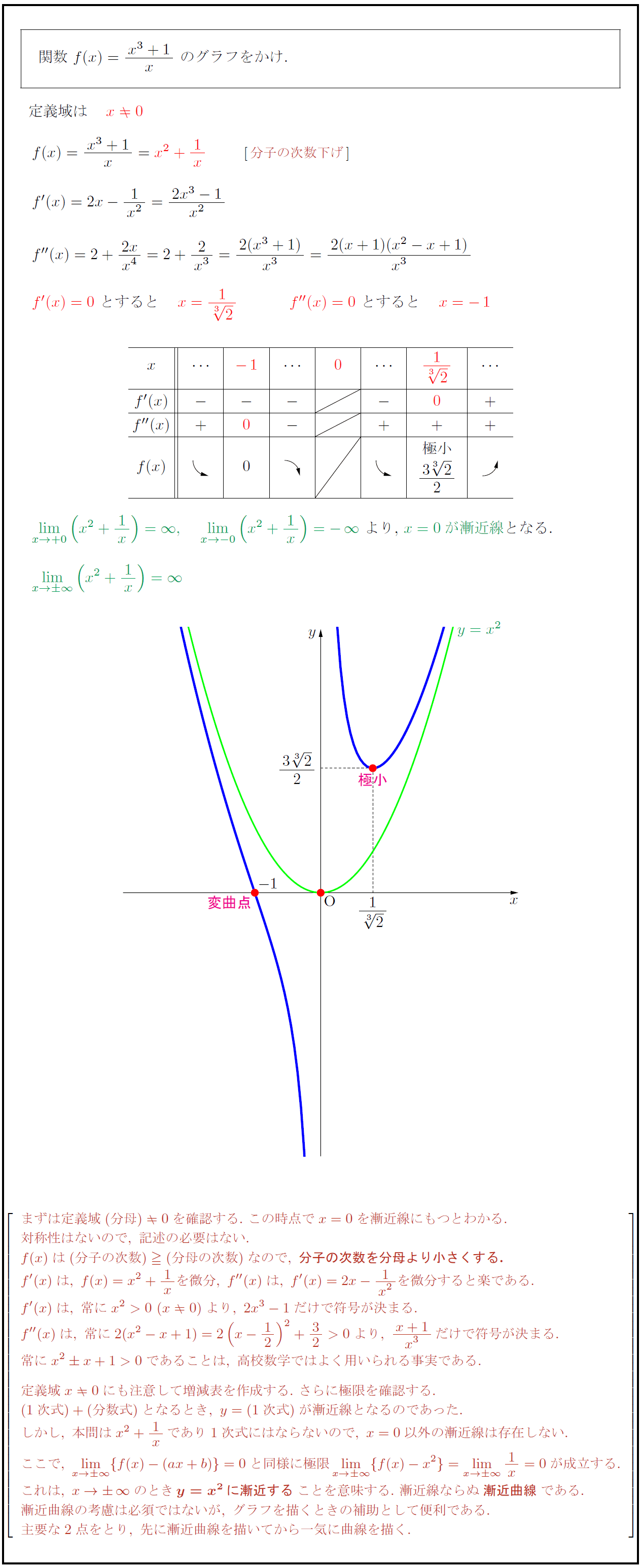
まずは定義域(分母)0を確認する.\ この時点でx=0を漸近線にもつとわかる. 対称性はないので,\ 記述の必要はない. f(x)は(分子の次数)(分母の次数)なので,\ {分子の次数を分母より小さくする.} f'(x)は,\ f(x)=x²+1xを微分,\ f”(x)は,\ f'(x)=2x-{1}{x²}を微分すると楽である. f'(x)は,\ 常にx²>0\ (x0)より,\ 2x³-1だけで符号が決まる. f”(x)は,\ 常に2(x²-x+1)=2(x-12)²+32>0より,\ {x+1}{x³}だけで符号が決まる. 常にx² x+1>0であることは,\ 高校数学ではよく用いられる事実である. 定義域x0にも注意して増減表を作成する.\ さらに極限を確認する. (1次式)+(分数式)となるとき,\ y=(1次式)が漸近線となるのであった. しかし,\ 本問はx²+1xであり1次式にはならないので,\ x=0以外の漸近線は存在しない. ここで,\ lim[x→∞]{f(x)-(ax+b)}=0と同様に極限lim[x→∞]{f(x)-x²}=lim[x→∞]1x=0が成立する. これは,\ x→∞ のとき{y=x²に漸近する}ことを意味する.\ 漸近線ならぬ{漸近曲線}である. 漸近曲線の考慮は必須ではないが,\ グラフを描くときの補助として便利である. 主要な2点をとり,\ 先に漸近曲線を描いてから一気に曲線を描く.

