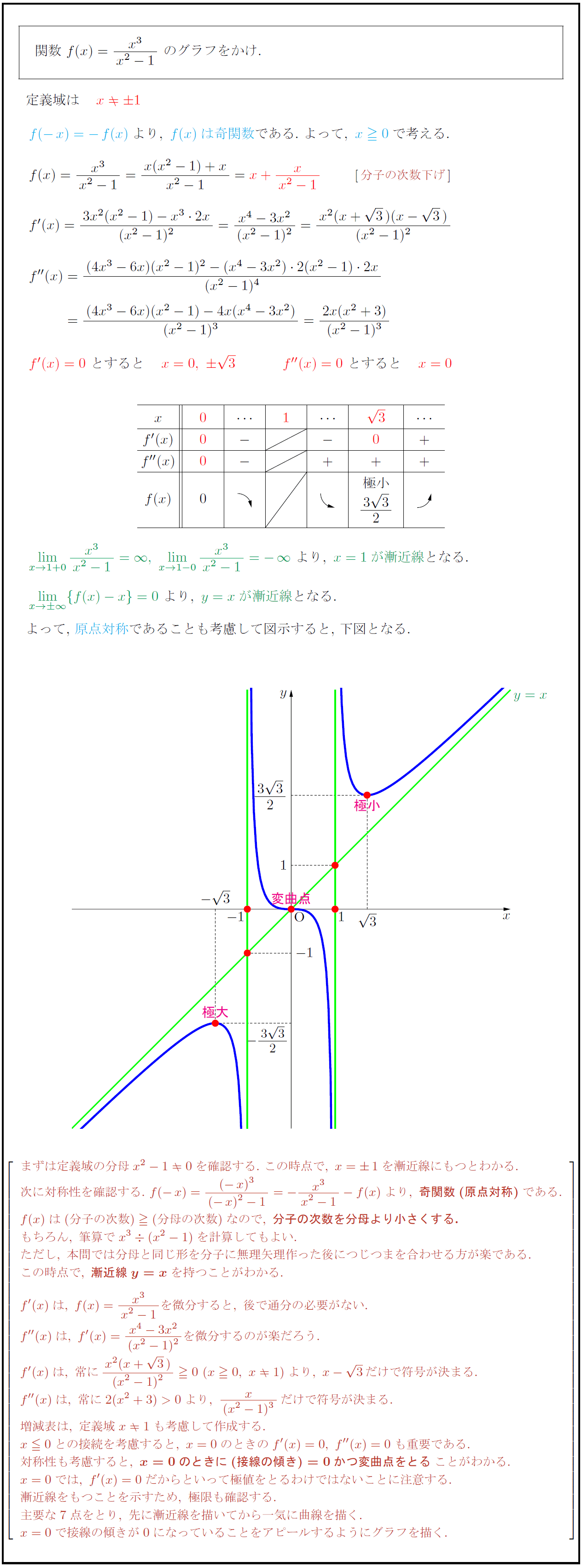
まずは定義域の分母x²-10を確認する.\ この時点で,\ x=1を漸近線にもつとわかる. 次に対称性を確認する.\ f(-x)={(-x)³}{(-x)²-1}=-{x³}{x²-1}-f(x)より,\ {奇関数(原点対称)}である. f(x)は(分子の次数)(分母の次数)なので,\ {分子の次数を分母より小さくする.} もちろん,\ 筆算でx³(x²-1)を計算してもよい. ただし,\ 本問では分母と同じ形を分子に無理矢理作った後につじつまを合わせる方が楽である. この時点で,\ {漸近線y=x}を持つことがわかる. f'(x)は,\ f(x)={x³}{x²-1}を微分すると,\ 後で通分の必要がない. f”(x)は,\ f'(x)={x⁴-3x²}{(x²-1)²}を微分するのが楽だろう. f'(x)は,\ 常に{x²(x+3)}{(x²-1)²}0\ (x0,\ x1)より,\ x-3だけで符号が決まる. f”(x)は,\ 常に2(x²+3)>0より,\ {x}{(x²-1)³}だけで符号が決まる. 増減表は,\ 定義域x1も考慮して作成する. x0との接続を考慮すると,\ x=0のときのf'(x)=0,\ f”(x)=0も重要である. 対称性も考慮すると,\ {x=0のときに(接線の傾き)=0かつ変曲点をとる}ことがわかる. x=0では,\ f'(x)=0だからといって極値をとるわけではないことに注意する. 漸近線をもつことを示すため,\ 極限も確認する. 主要な7点をとり,\ 先に漸近線を描いてから一気に曲線を描く. x=0で接線の傾きが0になっていることをアピールするようにグラフを描く.

