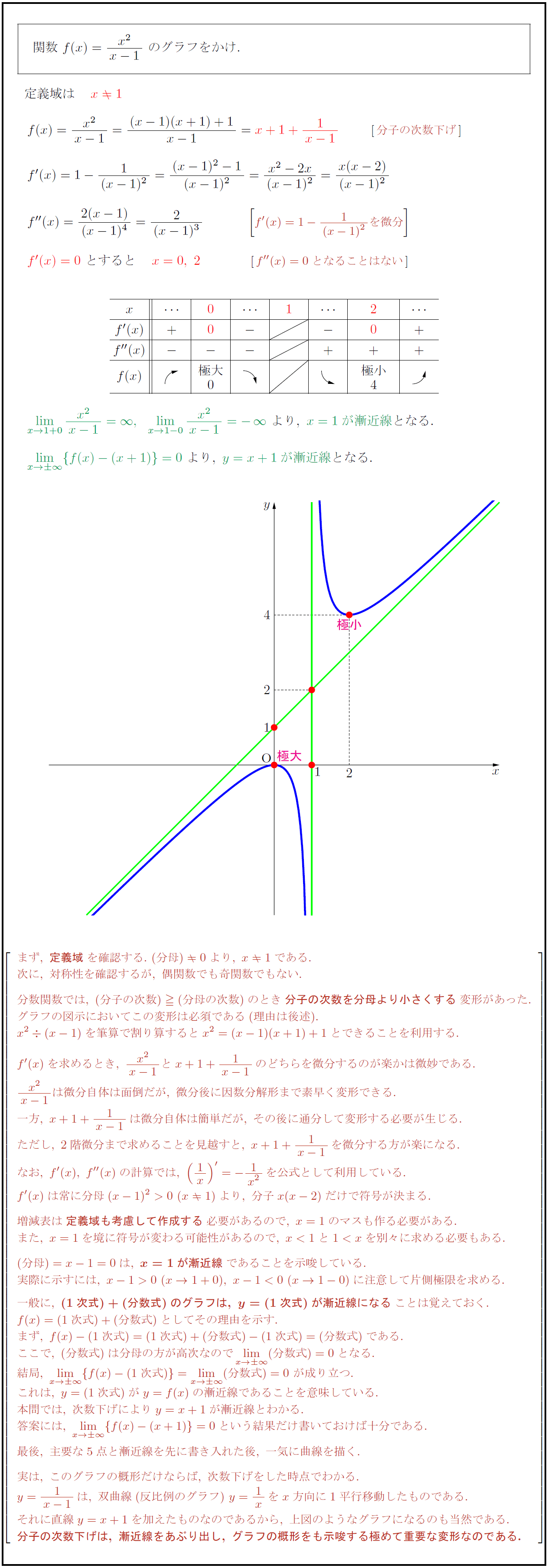
関数\ f(x)={x²}{x-1}\ のグラフをかけ.$ 定義域は ,分子の次数下げ}]$} 極大 }極小 }{y=x+1が漸近線}となる.$ まず,\ {定義域}を確認する.\ (分母)0より,\ x1である. 次に,\ 対称性を確認するが,\ 偶関数でも奇関数でもない. 分数関数では,\ (分子の次数)(分母の次数)のとき{分子の次数を分母より小さくする}変形があった. グラフの図示においてこの変形は必須である(理由は後述). x²(x-1)を筆算で割り算するとx²=(x-1)(x+1)+1とできることを利用する. f'(x)を求めるとき,\ {x²}{x-1}とx+1+{1}{x-1}のどちらを微分するのが楽かは微妙である. {x²}{x-1}は微分自体は面倒だが,\ 微分後に因数分解形まで素早く変形できる. 一方,\ x+1+{1}{x-1}は微分自体は簡単だが,\ その後に通分して変形する必要が生じる. ただし,\ 2階微分まで求めることを見越すと,\ x+1+{1}{x-1}を微分する方が楽になる. なお,\ f'(x),\ f”(x)の計算では,\ (1x)’=-{1}{x²}を公式として利用している. f'(x)は常に分母(x-1)²>0\ (x1)より,\ 分子x(x-2)だけで符号が決まる. 増減表は{定義域も考慮して作成する}必要があるので,\ x=1のマスも作る必要がある. また,\ x=1を境に符号が変わる可能性があるので,\ x<1と10\ (x→1+0),\ x-1<0\ (x→1-0)に注意して片側極限を求める. 一般に,\ {(1次式)+(分数式)のグラフは,\ y=(1次式)が漸近線になる}ことは覚えておく. f(x)=(1次式)+(分数式)としてその理由を示す. まず,\ f(x)-(1次式)=(1次式)+(分数式)-(1次式)=(分数式)である. ここで,\ (分数式)は分母の方が高次なので lim[x→∞](分数式)=0となる. 結局,\ lim[x→∞]{f(x)-(1次式)}=lim[x→∞](分数式)=0\ が成り立つ. これは,\ y=(1次式)がy=f(x)の漸近線であることを意味している. 本問では,\ 次数下げによりy=x+1が漸近線とわかる. 答案には,\ lim[x→∞]{f(x)-(x+1)}=0という結果だけ書いておけば十分である. 最後,\ 主要な5点と漸近線を先に書き入れた後,\ 一気に曲線を描く. 実は,\ このグラフの概形だけならば,\ 次数下げをした時点でわかる. y={1}{x-1}は,\ 双曲線(反比例のグラフ)\ y=1xをx方向に1平行移動したものである. それに直線y=x+1を加えたものなのであるから,\ 上図のようなグラフになるのも当然である. {分子の次数下げは,\ 漸近線をあぶり出し,\ グラフの概形をも示唆する極めて重要な変形なのである.}

