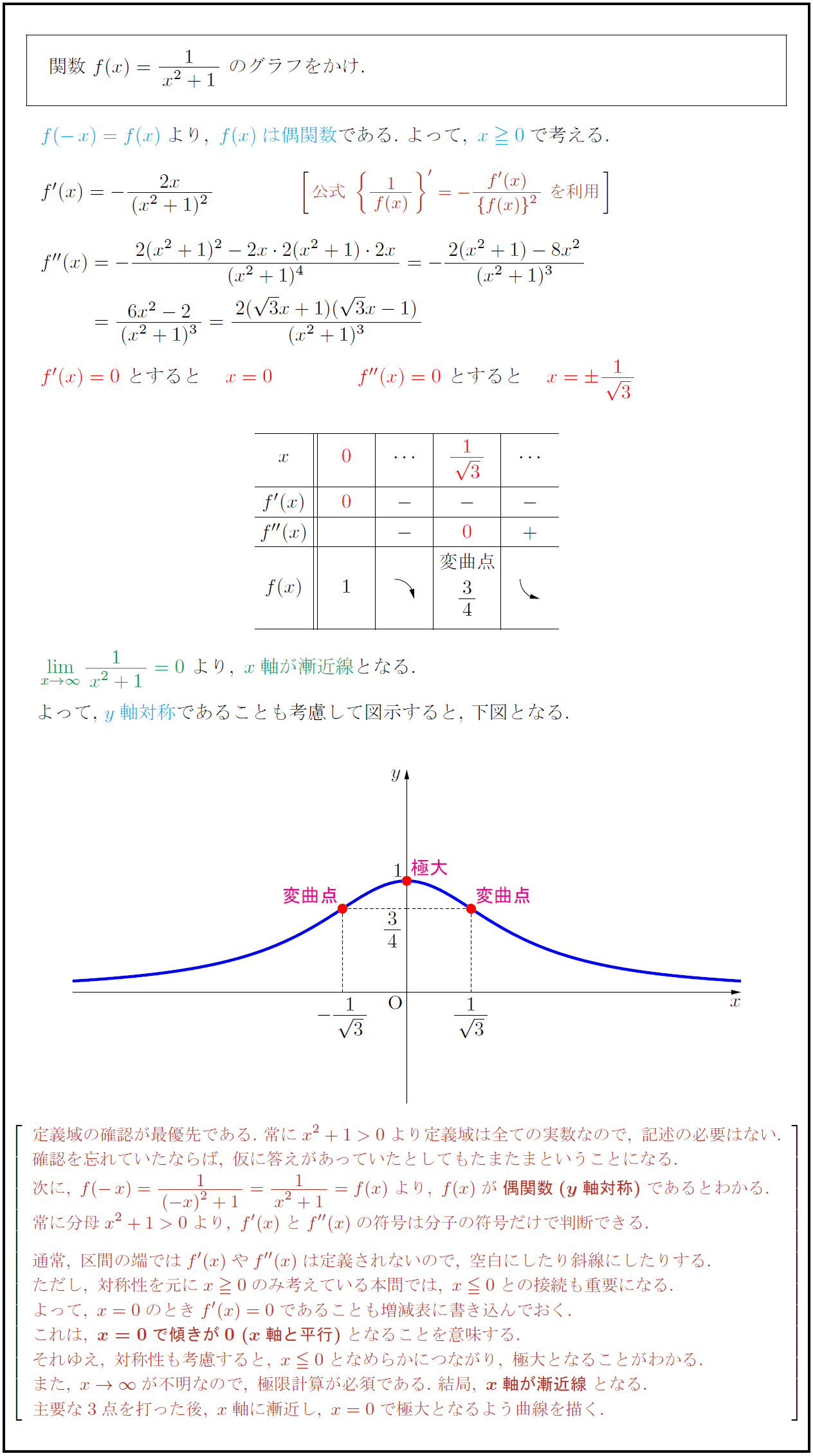
関数\ f(x)={1}{x²+1}\ のグラフをかけ.$ f(x)は偶関数}である.\ よって,\ x0}で考える.$ {x軸が漸近線}となる.$ よって,\ $y$軸対称}であることも考慮して図示すると,\ 下図となる. \極大変曲点} 定義域の確認が最優先である.\ 常にx²+1>0より定義域は全ての実数なので,\ 記述の必要はない. 確認を忘れていたならば,\ 仮に答えがあっていたとしてもたまたまということになる. 次に,\ f(-x)={1}{(-x)²+1}={1}{x²+1}=f(x)より,\ f(x)が{偶関数(y軸対称)}であるとわかる. 常に分母x²+1>0より,\ f'(x)とf”(x)の符号は分子の符号だけで判断できる. 通常,\ 区間の端ではf'(x)やf”(x)は定義されないので,\ 空白にしたり斜線にしたりする. ただし,\ 対称性を元にx0のみ考えている本問では,\ x0との接続も重要になる. よって,\ x=0のときf'(x)=0であることも増減表に書き込んでおく. これは,\ {x=0で傾きが0\ (x軸と平行)}となることを意味する. それゆえ,\ 対称性も考慮すると,\ x0となめらかにつながり,\ 極大となることがわかる. また,\ x→∞ が不明なので,\ 極限計算が必須である.\ 結局,\ {x軸が漸近線}となる. 主要な3点を打った後,\ x軸に漸近し,\ x=0で極大となるよう曲線を描く.

