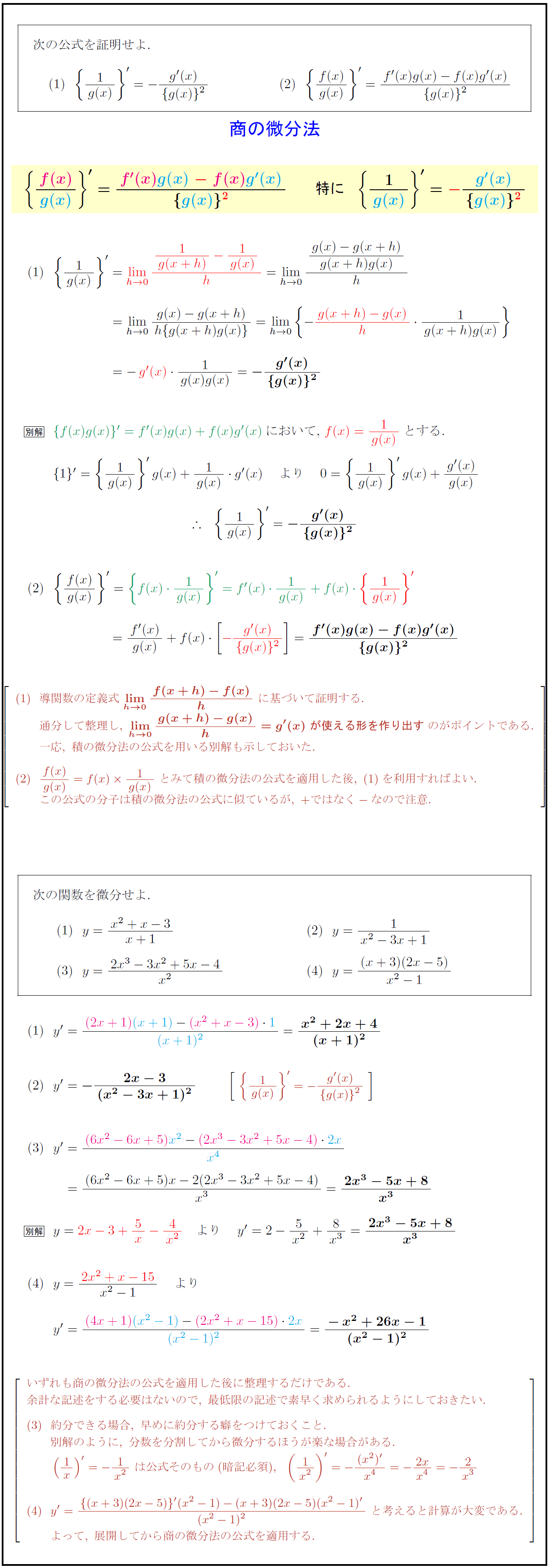
次の公式を証明せよ. $1}{g(x)’=-{g'(x)}g(x)}²}$ $f(x)}{g(x)’={f'(x)g(x)-f(x)g'(x)}g(x)}²}$ {商の微分法} 導関数の定義式\ {lim[h→0]{f(x+h)-f(x)}{h\ に基づいて証明する. 通分して整理し,\ {lim[h→0]{g(x+h)-g(x)}{h}=g'(x)\ が使える形を作り出す}のがポイントである. 一応,\ 積の微分法の公式を用いる別解も示しておいた. {f(x)}{g(x)}=f(x){1}{g(x)}\ とみて積の微分法の公式を適用した後,\ を利用すればよい. この公式の分子は積の微分法の公式に似ているが,\ +ではなく-なので注意. いずれも商の微分法の公式を適用した後に整理するだけである. 余計な記述をする必要はないので,\ 最低限の記述で素早く求められるようにしておきたい. 約分できる場合,\ 早めに約分する癖をつけておくこと. 別解のように,\ 分数を分割してから微分するほうが楽な場合がある. (1x)’=-{1}{x²}\ は公式そのもの(暗記必須),({1}{x²})’=-{(x²)’}{x⁴}=-{2x}{x⁴}=-{2}{x³} y’=(x+3)(2x-5)}'(x²-1)-(x+3)(2x-5)(x²-1)’}{(x²-1)²}\ と考えると計算が大変である. よって,\ 展開してから商の微分法の公式を適用する.

