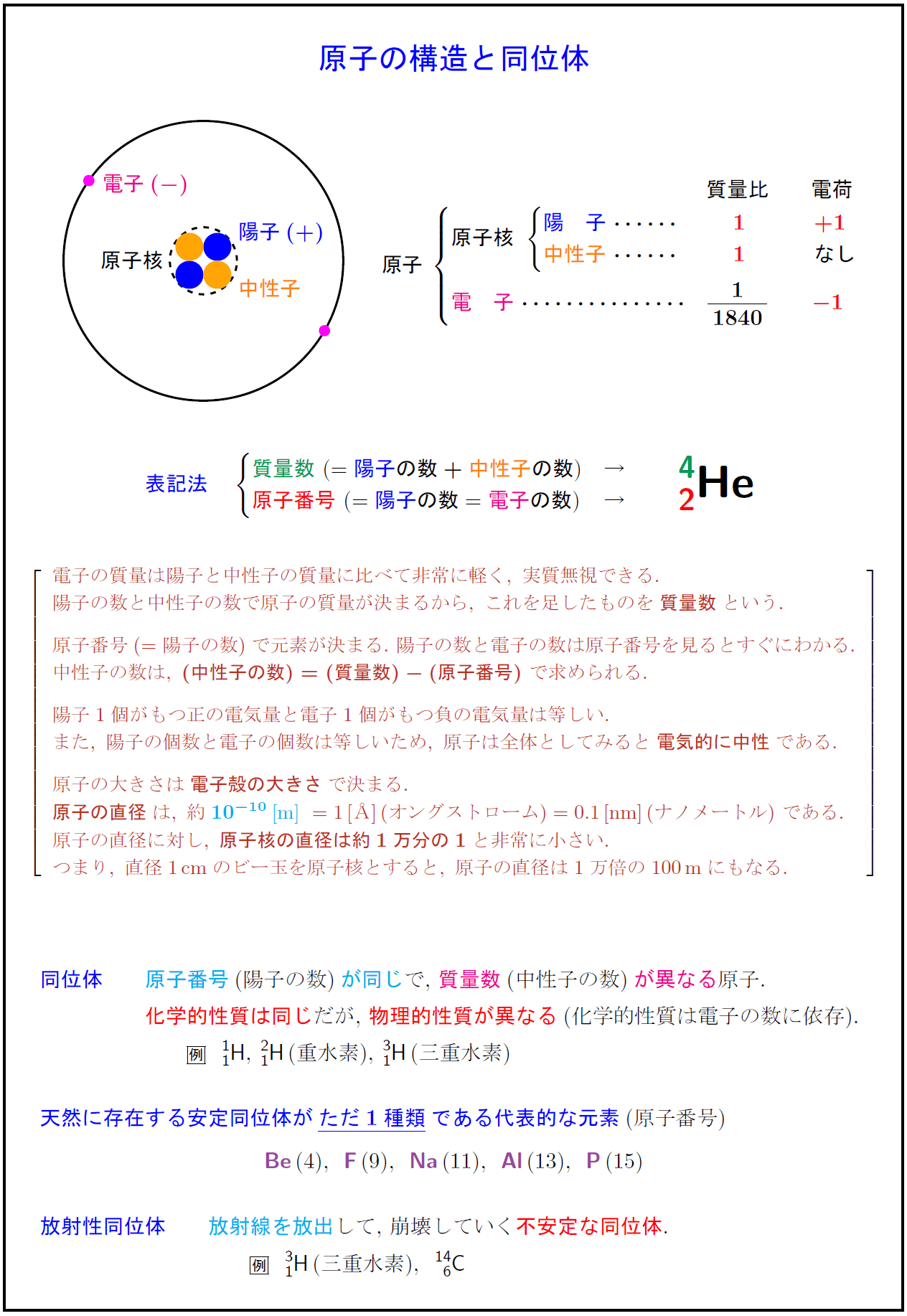
陽子(+)} 中性子} 電子(原子核 質量比} 電荷} 原子核\ 陽 子}\ \repeatstr{2} 1} +1} 中性子}\ \repeatstr{2} 1} なし 電 子}\ \repeatstr{5} {1}{1840} \表記法 質量数\ (={陽子}の数+中性子}の数}) {原子番号\ (={陽子}の数}={電子}の数}) 電子の質量は陽子と中性子の質量に比べて非常に軽く,\ 実質無視できる. 陽子の数と中性子の数で原子の質量が決まるから,\ これを足したものを{質量数}という. 原子番号(=陽子の数)で元素が決まる.\ 陽子の数と電子の数は原子番号を見るとすぐにわかる. 中性子の数は,\ {(中性子の数)=(質量数)-(原子番号)}\ で求められる. 陽子1個がもつ正の電気量と電子1個がもつ負の電気量は等しい. また,\ 陽子の個数と電子の個数は等しいため,\ 原子は全体としてみると{電気的に中性}である. 原子の大きさは{電子殻の大きさ}で決まる. {原子の直径}は,\ 約10^{-10}[m]}\ =1[Å]}(オングストローム)=0.1[nm]}(ナノメートル)\ である. 原子の直径に対し,\ {原子核の直径は約1万分の1}と非常に小さい. つまり,\ 直径1cm}のビー玉を原子核とすると,\ 原子の直径は1万倍の100m}にもなる. 同位体}原子番号(陽子の数)が同じで,\ 質量数(中性子の数)が異なる原子. 化学的性質は同じだが,\ 物理的性質が異なる(化学的性質は電子の数に依存). {^1₁H},\ {²₁H}(重水素),\ {³₁H}(三重水素) 安定同位体が存在しない}元素(原子番号) {Be},{F},{Na}(11),{Al}(13),{P}(15) 放射性同位体 放射線を放出して, 崩壊していく不安定な同位体. {³₁H}(三重水素),{^{14}_6C}

