

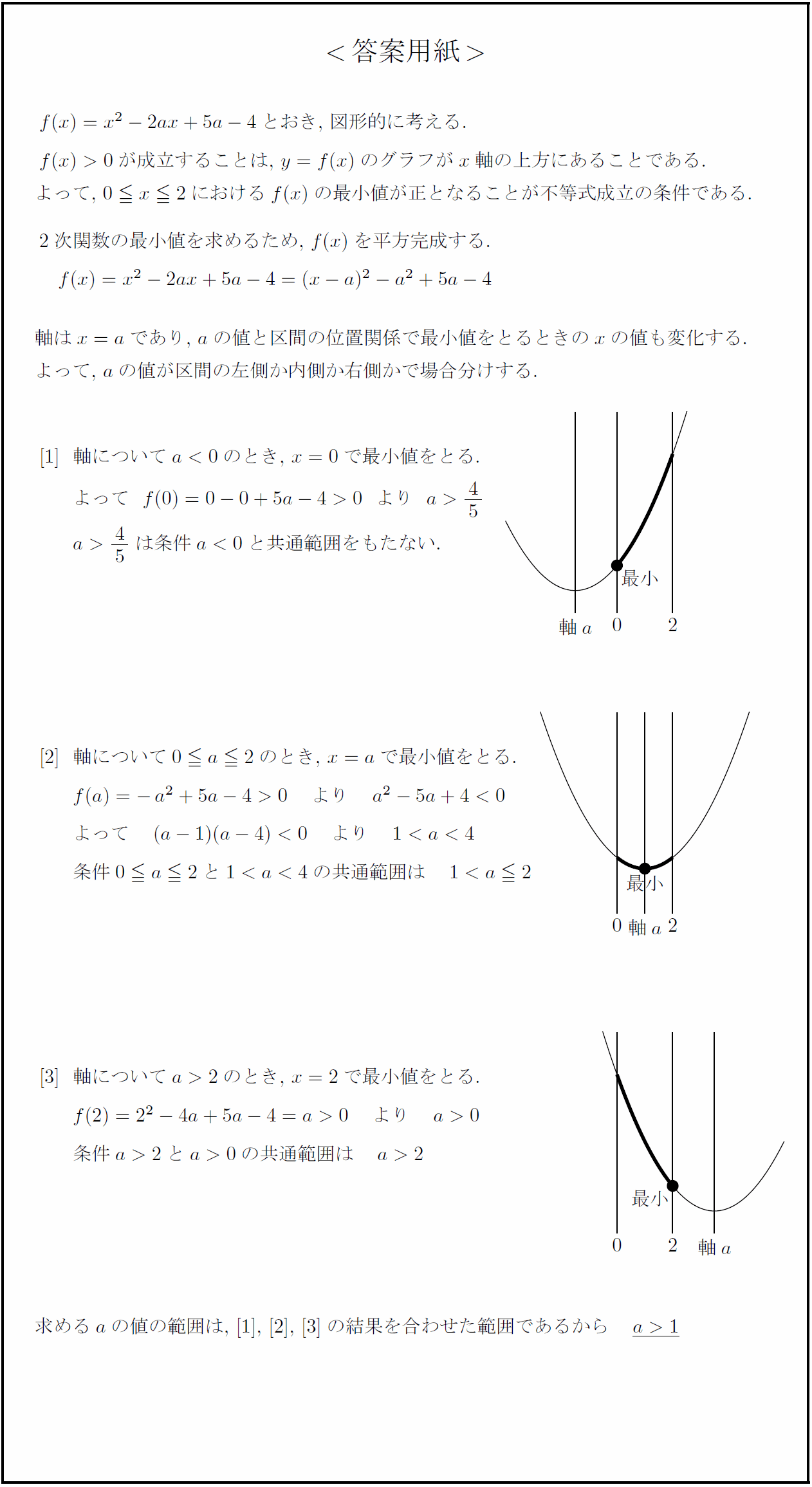

うな定数$a$の値の範囲を求めよ.
まず,\ ありがちな答案例を示す. <$答案用紙$>$
$x²-2ax+5a-4=(x-a)²-a²+5a-4$
$a<0$のとき $f(0)>0 より a>54$ (条件を満たさない)
$0 a2$のとき $f(a)>0 より 1
したがって $a>1$ [55zh]
{学生 「基本的な問題ですね.\ すぐにできました」}
教師 「友達に略解を示すのとは訳が違うのでわかるように説明して」}
学生 「採点官は数学のプロなのでこれだけで理解出来ると思うのですが」}
学生の主張にも一理あるような気がする.
しかし,\ 日本語での説明が不足しているものは本番の答案として不適切である.
理由は後で述べるとして,\ 個人的に推奨したい解答とその理由を先に示す.
答案用紙$>$
$f(x)=x²-2ax+5a-4$とおき,\ 図形的に考える.
$f(x)>0$が成立することは,\ $y=f(x)$のグラフが$x$軸の上方にあることである.
よって,\ $0 x2$における$f(x)$の最小値が正となることが不等式成立の条件である.
2次関数の最小値を求めるため,\ $f(x)$を平方完成する.
$f(x)=x²-2ax+5a-4=(x-a)²-a²+5a-4$
軸は$x=a$であり,\ $a$の値と区間の位置関係で最小値をとるときの$x$の値も変化する.
よって,\ $a$の値が区間の左側か内側か右側かで場合分けする.
軸について$a<0$のとき,\ $x=0$で最小値をとる. { }よって$f(0)=0-0+5a-4>0よりa>45$
{ }$a>45$は条件$a<0$と共通範囲をもたない. [8zh] 軸について$0 a2$のとき,\ $x=a$で最小値をとる. { }$f(a)=-a²+5a-4>0 より a²-5a+4<0$ { }$よって (a-1)(a-4) { }$条件0 a2 と1
{ }$f=2²-4a+5a-4=a>0 より a>0$
{ }$条件a>2とa>0の共通範囲は a>2$ [8zh]
求める$a$の値の範囲は,\ ,\ ,\ [3]の結果を合わせた範囲であるから
この答案のポイントを列挙していく.
全体を通して言えるのは,\ 過剰とも感じる説明と採点官へのアピールである.
\begin{itemize}
\item 最初の答案では突然$f(0)$などが出てくるが,\ 「$f(x)$って何?」と言いたくなる.
新たな文字を持ち出す場合,\ その定義を最初に明記すべきである. ₀
\item 解法の方針,\ 使用する公式・定理,\ 最終目標などをあらかじめ日本語で説明する.}
完遂できなかったり,\ 計算ミスがあったとしても,\ 部分点がもらえる可能性が残る.
数式しか書いてなかった場合,\ 立式ミスでもしようものなら一巻の終わりである.
特に,\ 場合の数・確率分野で式だけ($34!+5=77$)は非常に危険である.
また,\ 自分自身に対しても方針を明確にし,\ 思考を整理する効果をもつ.
計算に集中している間に何を目指していたのかを忘れてしまうといったことを防げる.
以上の考え方は,\ 推奨答案の次の点で用いられている. [-2zh]
\begin{enumerate}
\item 図形的に考えて問題を解くことを最初に明記して採点官にアピールしている.
さらに,\ 図形的にどう考えられるのか,\ 結局どうすべきなのかまで示している. [-1.3zh]
\item 平方完成する旨,\ さらにその理由を先に記述している. [-1.3zh]
\item 何故場合分けするのか,\ さらにどのように場合分けするのかを先に記述している.{可能な限り図・グラフ・表を描く.}\ 採点官にも自分にも視覚的にわかりやすい.
記述ミスや計算ミスがあった場合でも,\ 部分点をもらえる可能性が残る. ₀
\item 途中計算も可能な限り示す.}
計算結果しか書いてなければ,\ それが間違っていた場合に全く評価されなくなる.
途中過程が示してあれば,\ 部分点をもらえる可能性が残る.
何より,\ 自分自身が後で見直したり修正したりする場合に役立つ. ₀
\item 共通範囲(かつ)と合わせた範囲(または)の違いを理解していることをアピール. ₀
\item とにかくわかりやすく,\ 見やすくなるよう体裁を整える(人間が採点するのだから).
特別な決まりはないので,\ 見る人の立場で工夫する. [-2zh]
\begin{enumerate}
\item ,\ }と番号を振るなどして場合分けを見やすくする.
\item 「よって」「つまり」「$\ (ゆえに)$」など,\ 論理の接続詞や記号を適度に使用する.
\item 式に番号をつけたり,\ 指摘部分まで矢印をのばたりする.
最終的な答えにはアンダーラインを引くなどして採点官にアピールする.
以上のような点に注意して記述することで,\ 部分点の可能性も上がると思われる.
ただし,\ これは数学の試験であり,\ 記述の仕方は本質的なものではない.
細かい記述の意識よりも, 答えに至ることが最重要であることを忘れてはならない.
さて,\ なぜ数学のプロである採点官に対してここまで丁寧に説明すべきなのだろうか.
要点さえ書いてあれば理解できるはずなのに.
実は,\ 理解できていないのにたまたま合っていたというケースが少なくない.
教師 「何故$a<0,\ 0 a2,\ a>2$と場合分けしたの?」
学生 「$a$を含む2次関数の最小は,\ $a$が区間の内か外かで場合分けすると覚えていました」
教師 「いや,\ 軸が$a$だからなんだけど$$」
ある受験生や採点官にとって当たり前でも,\ そうではない受験生が一定数存在する.
そのような現状で,\ 記述不足の答案を採点官がみたらどう思うだろうか.
「もしかしてこの受験生もたまたま合っていただけなのでは$$」と思われないだろうか.
採点官は行間を読んでくれる,\ 意図を読み取ってくれるなどというのは希望的憶測である.
むしろ,\ 採点官は受験生の思考を推測したり予想したりすべきではない.
答案に書いてあるものだけで判断すべきである.
このとき,\ どちらともとれるような答案はわかっていないものとみなさざるを得ない.
よって,\ 受験生は一切の疑念の余地がない丁寧な答案を記述すべきなのである.
また,\ 本番は相対評価,\ つまり他受験生との比較である.
もし他の受験生が皆,\ 意図が明確に伝わるような丁寧な記述をしていたらどうなるだろう.
当然と思って記述を省いていると,\ 単にできない受験生と同等に評価される可能性がある.
逆に,\ 丁寧に記述しておけば,\ わかっていない受験生と明確に差別化を図ることができる.
相対評価なのであるから,\ それが結果として加点につながることにもなるだろう.
結局,\ 「採点官が理解できるか否か」という問題ではない.
「採点官が,\ 受験生本人が理解できているかを確認できるか}」}という問題である.
「プロなんだからこれでわかるでしょ?」とも言わんばかりの答案ではいけない.
採点官が能力確認できるような記述を謙虚な姿勢で行うことが重要である.

