媒介変数⑥　対数螺旋（等角螺旋）x=e^θcosθ,　y=e^θsinθ

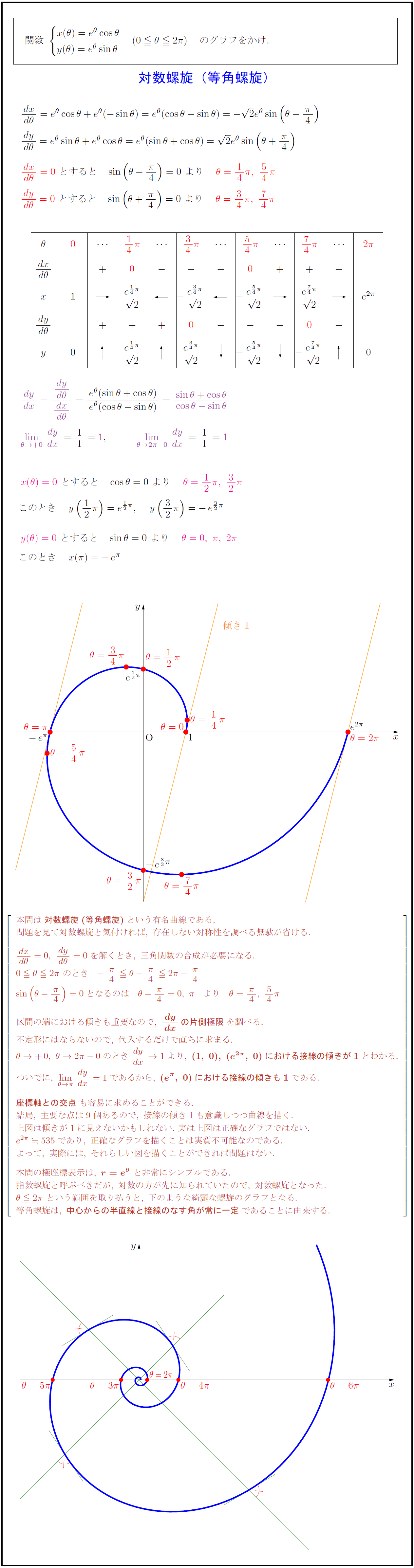
本問は{対数螺旋(等角螺旋)}という有名曲線である. 問題を見て対数螺旋と気付ければ,\ 存在しない対称性を調べる無駄が省ける. {dx}{dθ}=0,\ {dy}{dθ}=0を解くとき,\ 三角関数の合成が必要になる. 0θ2π\ のとき-{π}{4}θ-{π}{4}2π-{π}{4} sin(θ-{π}{4})=0となるのは　θ-{π}{4}=0,\ π　より　θ={π}{4},\ 54π 区間の端における傾きも重要なので,\ dy}{dx}の片側極限}を調べる. 不定形にはならないので,\ 代入するだけで直ちに求まる. θ→+0,\ θ→2π-0のとき{dy}{dx}→1より,\ {(1,\ 0),\ (e^{2π},\ 0)における接線の傾きが1}とわかる. ついでに,\ limθ→π}{dy}{dx}=1であるから,\ {(e^π,\ 0)における接線の傾きも1}である. {座標軸との交点}も容易に求めることができる. 結局,\ 主要な点は9個あるので,\ 接線の傾き1も意識しつつ曲線を描く. 上図は傾きが1に見えないかもしれない.\ 実は上図は正確なグラフではない. e^{2π}535であり,\ 正確なグラフを描くことは実質不可能なのである. よって,\ 実際には,\ それらしい図を描くことができれば問題はない. 本問の極座標表示は,\ {r=e^θ}\ と非常にシンプルである. 指数螺旋と呼ぶべきだが,\ 対数の方が先に知られていたので,\ 対数螺旋となった. θ2π\ という範囲を取り払うと,\ 下のような綺麗な螺旋のグラフとなる. 等角螺旋は,\ {中心からの半直線と接線のなす角が常に一定}であることに由来する.