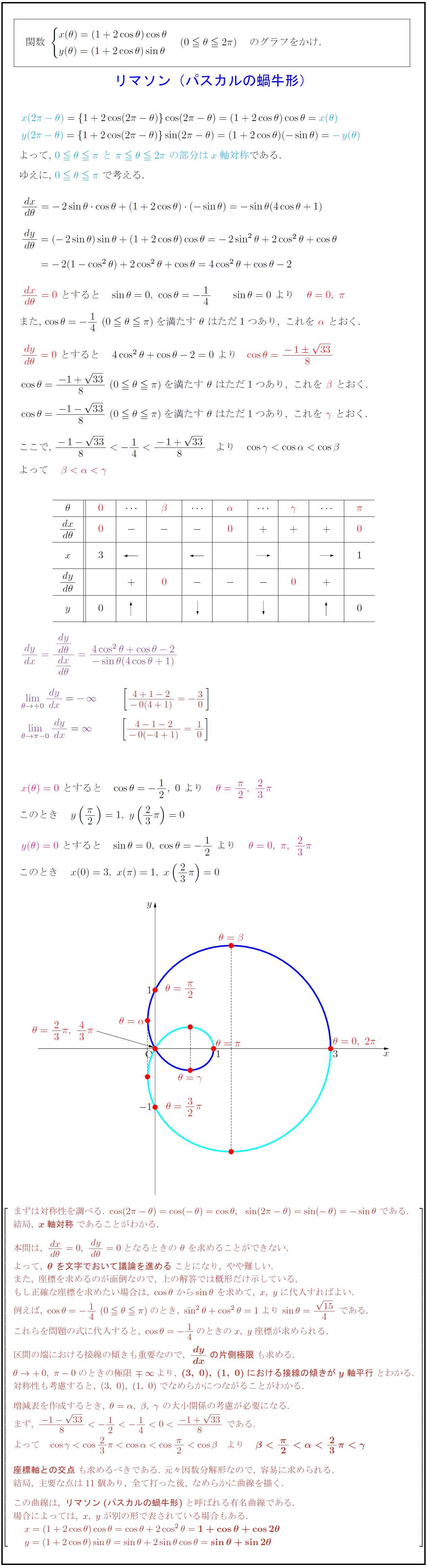
まずは対称性を調べる.\ cos(2π-θ)=cos(-θ)=cosθ,sin(2π-θ)=sin(-θ)=-sinθ\ である. 結局,\ {x軸対称}であることがわかる. 本問は,\ {dx}{dθ}=0,\ {dy}{dθ}=0となるときの\ θ\ を求めることができない. よって,\ {θ\ を文字でおいて議論を進める}ことになり,\ やや難しい. また,\ 座標を求めるのが面倒なので,\ 上の解答では概形だけ示している. もし正確な座標を求めたい場合は,\ cosθ\ からsinθ\ を求めて,\ x,\ yに代入すればよい. これらを問題の式に代入すると,\ cosθ=-14のときのx,\ y座標が求められる. 区間の端における接線の傾きも重要なので,\ dy}{dx}の片側極限}も求める. θ→+0,\ π-0のときの極限±∞より,\ {(3,\ 0),\ (1,\ 0)における接線の傾きがy軸平行}とわかる. 対称性も考慮すると,\ (3,\ 0),\ (1,\ 0)でなめらかにつながることがわかる. 増減表を作成するとき,\ θ=α,\ β,\ γ\ の大小関係の考慮が必要になる. {座標軸との交点}も求めるべきである.\ 元々因数分解形なので,\ 容易に求められる. 結局,\ 主要な点は11個あり,\ 全て打った後,\ なめらかに曲線を描く. この曲線は,\ {リマソン(パスカルの蝸牛形)}と呼ばれる有名曲線である. 場合によっては,\ x,\ yが別の形で表されている場合もある.

