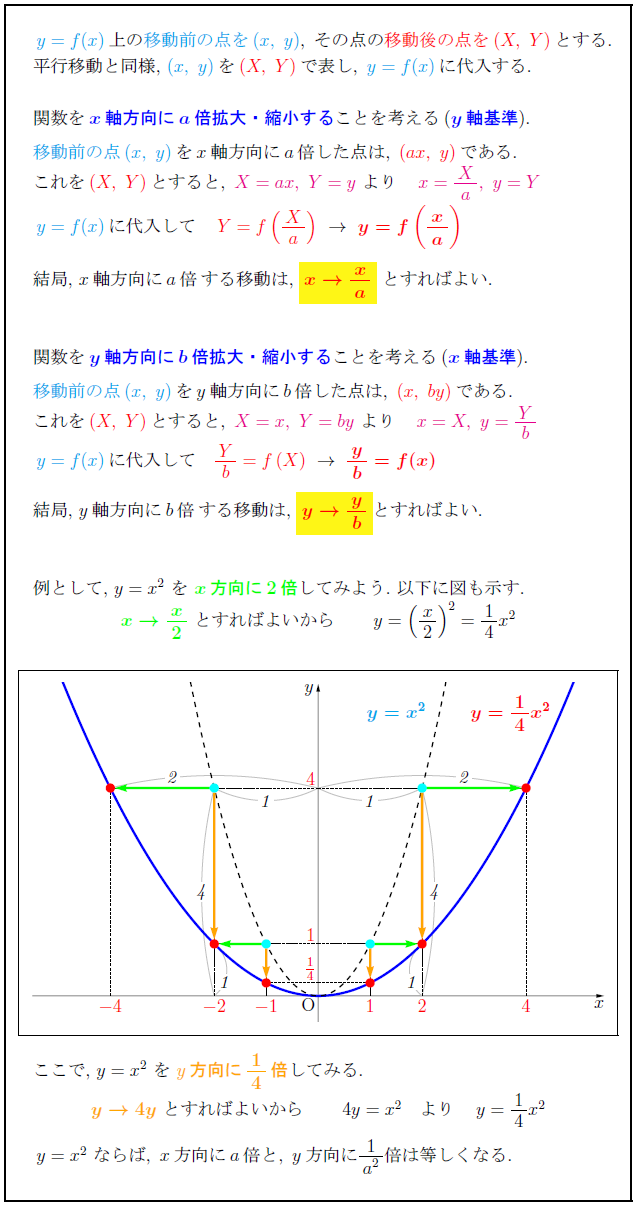
移動前の点を(x,\ y)},\ その点の移動後の点を(X,\ Y)}とする.$ 平行移動と同様,\ $(x,\ y)}を(X,\ Y)}で表し,\ y=f(x)}に代入する.$ 関数を${x軸方向にa倍拡大・縮小することを考える({y軸基準).$ 移動前の点}$(x,\ y)}をx軸方向にa倍した点は,\ (ax,\ y)}である.$ これを$(X,\ Y)}とすると,\ X=ax,\ Y=y}\ より x={X}{a},\ y=Y}$ $y=f(x)}に代入して 結局,\ $x軸方向にa倍$する移動は,\ yellow}{${x→ xa$}\ とすればよい. 関数を${y軸方向にb倍拡大・縮小することを考える({x軸基準).$ 移動前の点}$(x,\ y)}をy軸方向にb倍した点は,\ (x,\ by)}である.$ \ 結局,\ $y軸方向にb倍$する移動は,\ yellow}{${y→ yb$}とすればよい. 例として,\ $y=x²\ を\ {x方向に2倍してみよう.\ 以下に図も示す.$ ここで,\ $y=x²$\ を\ $y$方向に${14}$倍してみる. ${y→4y\ とすればよいから 4y=x² より y=14x²$} $y=x²\ ならば,\ x方向にa倍と,\ y方向に{1}{a²}倍は等しくなる.$

