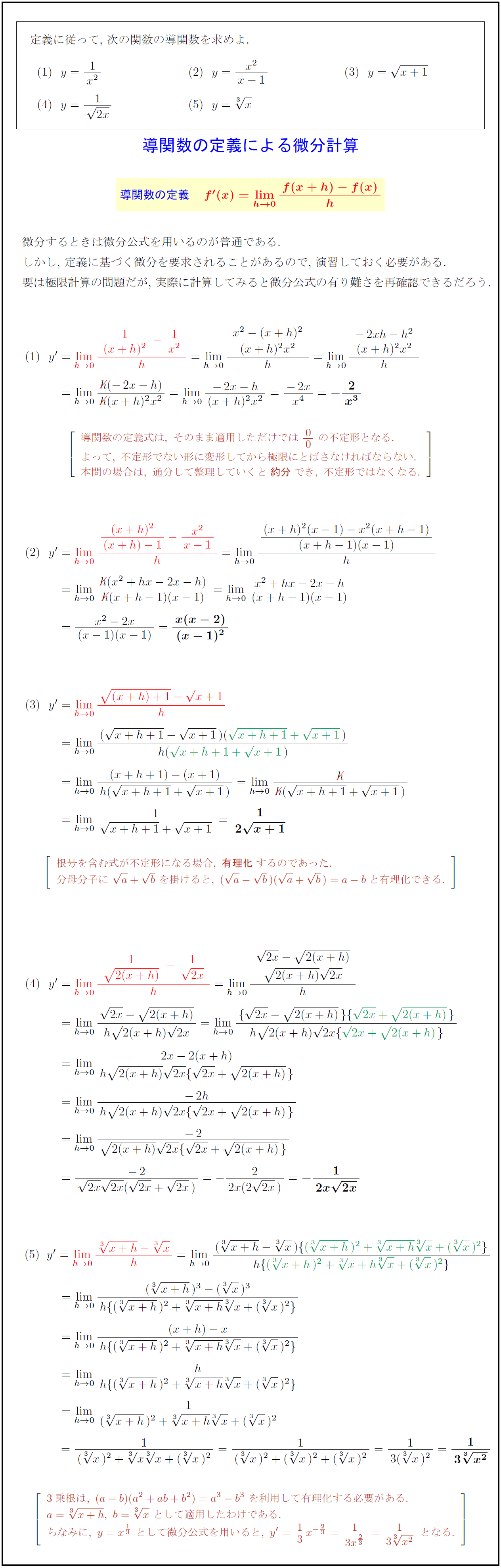
定義に従って,\ 次の関数の導関数を求めよ. {導関数の定義による微分計算導関数の定義} ${f'(x)=lim[h→0]{f(x+h)-f(x)}{h$ 微分するときは微分公式を用いるのが普通である. しかし,\ 定義に基づく微分を要求されることがあるので,\ 演習しておく必要がある. 要は極限計算の問題だが,\ 実際に計算してみると微分公式の有り難さを再確認できるだろう. 導関数の定義式は,\ そのまま適用しただけでは\ 00\ の不定形となる. よって,\ 不定形でない形に変形してから極限にとばさなければならない. 本問の場合は,\ 通分して整理していくと{約分}でき,\ 不定形ではなくなる. 根号を含む式が不定形になる場合,\ {有理化}するのであった. 分母分子に\ a+ b\ を掛けると,\ ( a- b)( a+ b)=a-bと有理化できる. 3乗根は,\ (a-b)(a²+ab+b²)=a³-b³\ を利用して有理化する必要がある. a=[3]{x+h},\ b=[3]{x}\ として適用したわけである. ちなみに,\ y=x^{1/3}\ として微分公式を用いると,\ y’=13x^{-2/3}={1}{3x^{2/3={1}{3[3]{x²\ となる.

