数学検定準1級を受けてみた。
サイトでネタとして取り上げるためである。
以下では、数学検定の概要と共に実際に受けたときの状況や受けてみての感想を述べる。
数学検定の概要
細かいことは級によっても違っていたりするので、必要ならば自分で公式サイト 実用数学技能検定(数学検定・算数検定) を確認してほしい。
とりあえず、自分が受検した準1級(高校3年程度、受検料4500円)の概要について簡単に述べる。1級(大学程度、受検料5000円)も同じである。試験時間、問題数、受検料などが微妙に違うが、大まかには2級(高校2年程度)、準2級(高校1年程度)も同様である。
まず、計算技能を問う1次試験(60分)と数理技能を問う2次試験(120分)がある。いずれも記述式である。
1次試験は約70%、2次試験は約60%が合格ラインである。
1次試験は計算問題全7問(1問1点)が必須問題として出題され、5問完答(5点)が合格ラインである。記述といっても答えだけなので事実上部分点は存在しないと思われる。
2次試験は全7問のうち必須問題が2問、選択問題が2問の合計4問(1問1点)で、2完半くらい(2.5点)が合格ラインである。ただし、途中過程の記述も要求され、小数点以下の部分点が与えられるので、4問全部半分くらいとかでも合格できるかもしれない。
1次と2次の一方だけ合格した場合、次は合格できなかった方のみの受検で済む。
合格率は大体こんな感じ。
1級 10%以下
準1級 15~20%
2級 25~30%
準2級 35~40%
数学検定準1級は何の役に立つ?
合否判定において、数学検定を考慮する大学や短大が数百ある。ただし、ほぼ推薦の場合であり、一般合格を目指す場合には関係ない。公式サイトに数検を考慮する大学とどのように評価するのかが全て載っているので、必要なら確認してみてほしい。
後でまた述べるが、難関大学レベルの高校3年生にとって数検準1級合格はさほど難しい話ではない。英検でいえば2級相当である。
しかし、一般合格が難しいので推薦で大学合格を目指すという学生にとっては相当ハードルが高い。よって、推薦で有利になるために準1級合格を目指すというのは基本的には無理がある。そういう意味で、数検準1級が大学合格に役立つかと問われたら答えはNOである。2級なら割と簡単なのでとっておくのもよい。
では、大学に一般合格するために数検準1級合格を目指して勉強するというのはどうだろうか。つまり、数検の勉強が受験勉強にも役立つのかと問われたら、当然答えはYESである。
ただし、役立つか否かと効果的か否かは別である。大学一般合格を目指すならば、大学一般合格のための勉強をするのが最も近道であり、あえて数検合格を目指して勉強する必然性はない。もっとも、大学受験のための勉強も数検合格のための勉強も所詮は高校数学なので本質的には同じである。むしろ、普通に大学受験を目指して勉強していれば、勝手に数検準1級合格できる力が身につく。
詳しくは知らないが、就職活動で役立つといったこともまずないのではないか。とりあえず履歴書に書けるくらいである。大卒が高校卒業程度の数検準1級や英検2級を履歴書に書いたところで採用上有利になるとは思えない。多少でも面接官に「ほう・・・」と思わせたいならば、少なくとも数検1級や英検準1級が必要である。高校卒業後すぐに就職とかなら有効かもしれない。
結局、数検準1級以下(英検2級以下)は、自己満足という側面がほとんどである。大学(一定以上のレベル)に合格できるということは、数検準1級や英検2級を持っていることに等しいからである。
数学検定準1級受検報告
1級と準1級は同じ部屋であった。男女比は6:4から7:3くらいだっただろうか。60歳以上と思われる高齢男性や1級を受けている男子小学生もいた。小学生は記念受験だったのか、ほとんど問題を解かないまま帰っていった。
まずは1次試験。単なる計算問題ばかりなので、特段考えることもなく20分くらいで解き終える。念のために見直しすると計算ミスしていたので慌てて修正(笑)。
過去問をみてわかってはいたが、瞬殺できる問題から結構厄介な問題まで難易度は様々。「現役の高校生にとっては結構シビアだなあ」などと物思いにふけりつつ30分ほど余った時間を過ごす。
2次試験開始。とりあえず全問をチラ見した後、必須問題から着手。すぐに、「これどこまで記述すればいいのかな」という記述試験特有の疑問が生じる。ということで、「さすがにここまで記述しておけば十分だろう」と思えるくらい結構慎重に記述する。30~40分ほどで4問完了。残り時間が少なくなるまでは退室もできないので、残りの3問も解いておく。
「サイトにどんな感じで載せようかな」などと考えていると退室可能な時間が来たので帰還することにした。答案を提出して帰り際、おそらく大学生と思われる女性が大学受験数学では使用を控えるべき裏技とされるロピタルの定理を使って解いていたのが見えた。大学生以上の受験生も多い数学検定では使っても何ら問題ないと思うが、適用条件の確認の問題があるので自分は避けた。
後日、ドキドキしながらサイトで合否確認する。
合格キタ━━━━━━(゚∀゚)━━━━━━!!!!
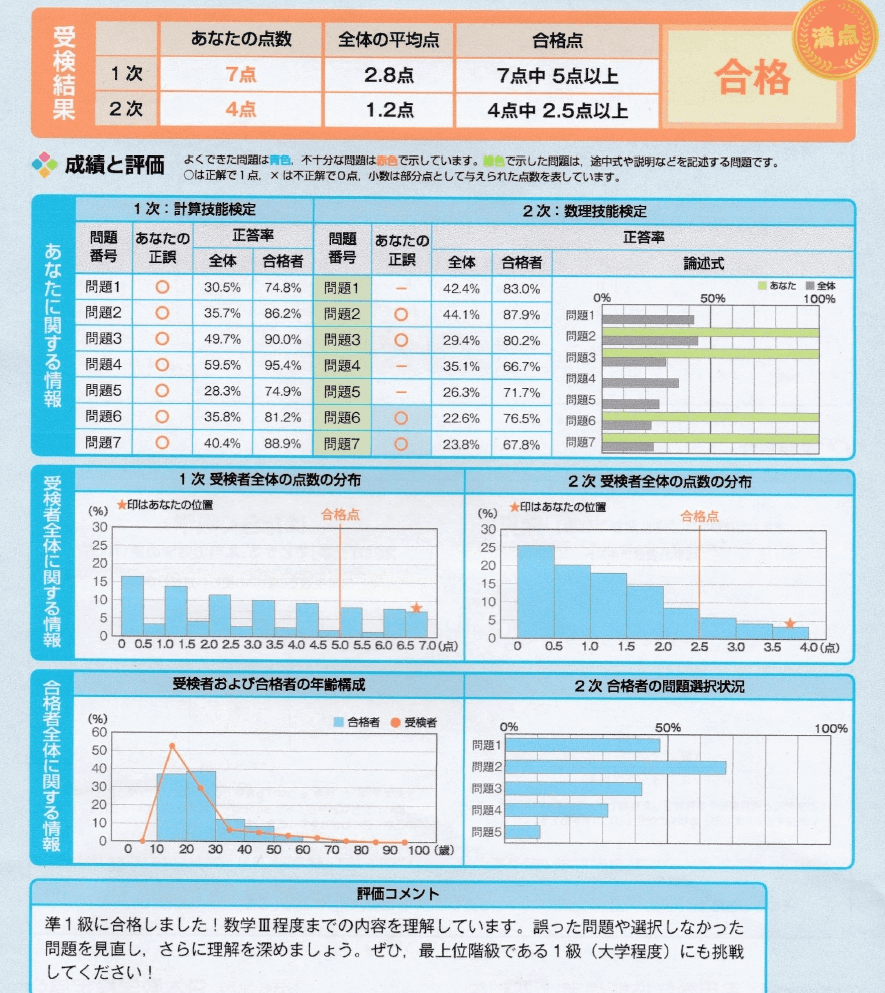
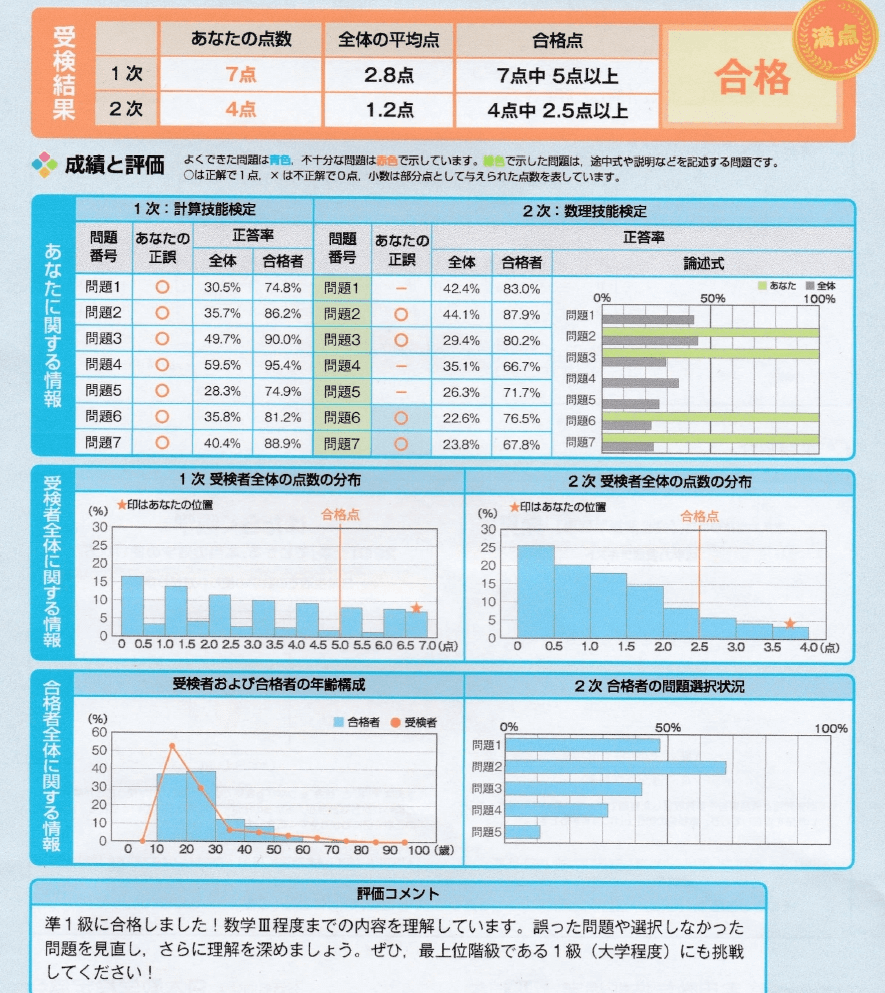
その後すぐに立派な合格証、合格証明書、個別成績表が届いた。
へえ~、満点って表示されるんだ~~~~∩( ・ω・)∩ばんじゃーい
数学検定準1級の難易度
多くの高校生や同程度のレベルの受検生にとっては結構難しい試験である。受検生の10代が約50%、20代以上が約50%という中で、20%以下という合格率も納得がいく。これは、英検2級の合格率約25%を下回る。多少なりとも数学が得意な受検生の中でこの合格率なのである。
まず、計算技能を問う1次試験が結構厄介である(合格率約30%)。7問すべてが必須問題で、60分間で5問の正解が要求される。答えだけなので少しでも違えばアウトである。やり方は合ってたのに最後の計算だけ間違えてしまったなどという失敗パターンもありえるだろう。計算技能とはいっても中にはやや応用的な問題もあり、高校数学全般の基本計算・基本事項・基本パターンが幅広く習得できているかが問われる。
2次試験も簡単ではない(合格率約15%)。時間的な余裕はあるのでじっくり考えることができるものの、問題難度は低いとはいえない。学校の定期試験レベルの学生はまず対応できないと思われる。選択問題は5問から自分が解けそうな2問を選んで解けばよいが、必須の2問が難しいとピンチである。学校の試験や大学受験であまり問われない数検独特の問題もあるので、そのような問題は普段数学の成績がよい学生でも手こずるだろう。
数Ⅲの学習が1通り完了していることを前提とすると、難易度の目安は以下のような感じになるだろうか。
難関国立大学レベルの理系 余裕
中堅国立大学レベルの理系 ギリいける
地方国立大学レベルの理系 きつい
数学検定準1級の対策
最も効果的な対策は、高校(一定レベル以上)で普通に授業を受けて出される課題をこなすことである。その上で、学校の進度にあわせて受検するのである。
ある程度の数学力をもつ高校生ならば、学校で数Ⅲの学習が終わった後で準1級を受ければ、最低限の労力で合格できる。特に何かする必要もない。せいぜい過去問を解いてみるということくらいのものである。準2級や2級も同様である。数ⅠA学習後に準2級、数ⅡB学習後に2級を受ければ割と容易に合格できるはずである。
公式サイトに出題範囲や過去1回分の問題と解答が載っているので、まずはどの程度対応できるかを確認するとよい。
準1級の出題範囲は、B(数Ⅲ)が50%、C(数ⅡB)が40%、その他が10%となっている。
実力が足りないと感じるならば、学校で与えられた問題集をやり直せばよい。
もし、学校の進度以上のレベルを独学でとなるとハードルは一気に高くなり、労力もかなりのものになる。
まずは、試験範囲を網羅学習しなければならない。しかし、数学検定用の問題集はどれも過去問に解答・解説を加えただけのものばかりであり、パターン網羅度は極めて低いので当てにならない。
そこで、大学受験を目指すほとんどの高校生が使ういわゆる網羅系問題集で学習することになる。
進学校御用達の青チャートやFocus Goldまでは必要なく、レベルが一段低い黄色チャートで十分だろう。
こんな分厚い問題集独学でやるのはきついという学生でも心配は無用である。そんな学生のために当サイトがあるのだから。受検に必要なことは当サイトの高校数学総覧に書いてある。
当サイトの基本+ちょい応用くらいまでの内容が身についていれば満点すら可能であることを今回証明した。
一通り網羅した後で、過去問題集を演習し、時間配分なども含めて最終確認すればよい。
では、数学検定合格を目指す諸君の健闘を祈る!