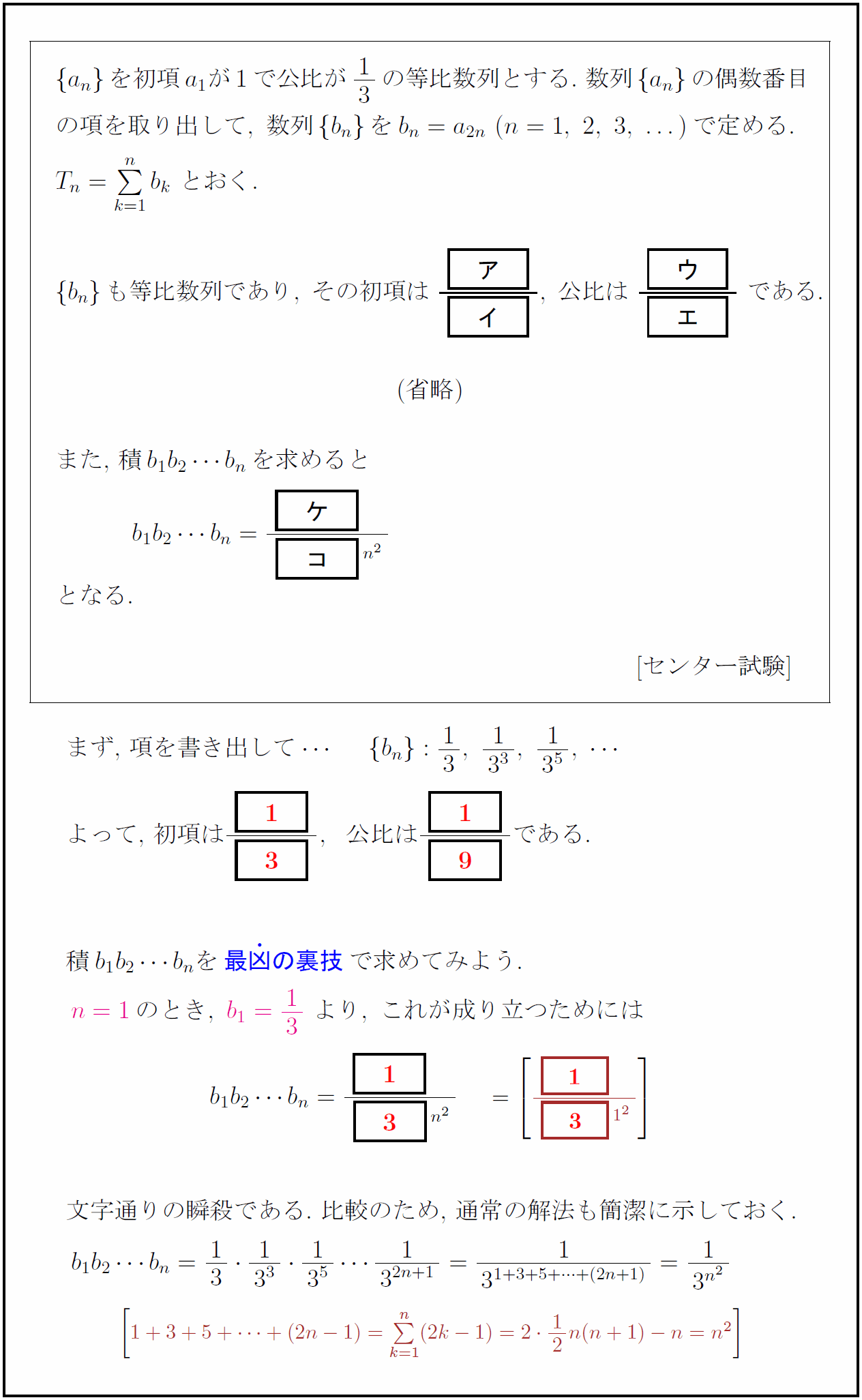
穴埋め式試験では十分性の確認がいらないことを悪用し、必要条件だけで答えを特定する凶悪な裏技である。
問題作成者の立場で言えば、穴埋め形式の試験である以上、この裏技を避けるのは簡単ではない。威力の凄まじさは、以下の例を見てもらえればわかるだろう。場合によっては、正攻法を知らなくても、圧倒的な速さで答えにたどり着ける。
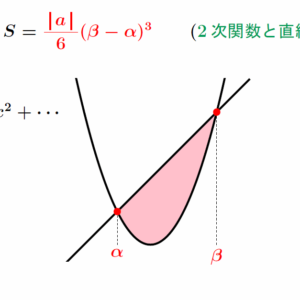
十分性がいらないなら、特殊な状況を考えて成り立つようにしてしまえばよい。特に三角関数の式変形や数列の問題においては極めて強力な裏技である。数列の問題にはいざというとき「n=1、2のときを考えろ」という格言もある。「全ての三角形で成り立つという条件なら、正三角形や直角二等辺三角形で考える」などと広く応用できる考え方である。
これを単に穴埋め式試験用の裏技と考えてはいけない。記述試験においても、「必要条件から攻める」という考え方は重要であり、よく使われるものである。難問では、必要条件だけでも求めて部分点を稼ぐという作戦も考えられる。もちろん、記述試験では十分条件の確認が必要になる。
大学入学共通テスト(センター数学)裏技的攻略法pdf★販売中
サイト上で公開している裏技には核心部分は含まれず、有料pdfの一部です。
有料pdfには、裏技の核心部分に加えて演習用の2006年以降の過去問の裏技的講評や数学以外の科目において最も当たりやすい数字は何かなども掲載しています。
