回転移動するには、基本的には複素数平面(数Ⅲ)か行列(新課程で消えた)を利用する。しかし、文系はいずれも学習しない。
入試にでは文系が回転移動を必要とすることはないが、複素数平面も行列も知らないならば、より根本に立ち戻って三角関数の加法定理を使うことになる。
原理そのものは平行移動や対称移動と同じである。
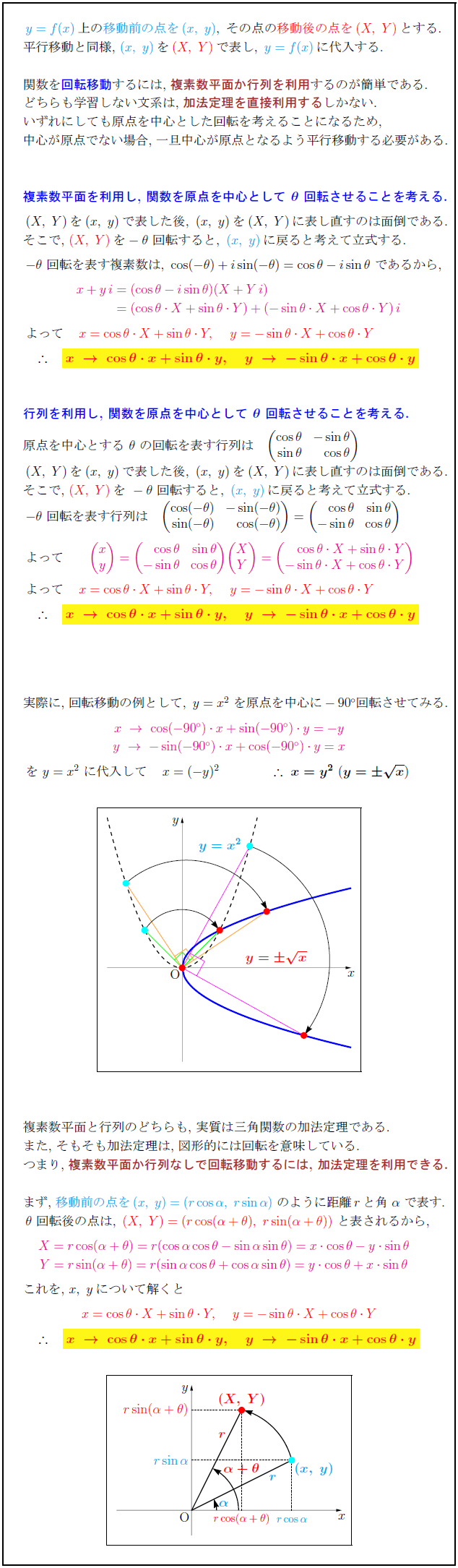
移動前の点を(x,\ y)},\ その点の移動後の点を(X,\ Y)}とする.$ 平行移動と同様,\ $(x,\ y)}を(X,\ Y)}で表し,\ y=f(x)}に代入する.$ 関数を回転移動するには,\ 複素数平面か行列を利用するのが簡単である. どちらも学習しない文系は,\ 加法定理を直接利用するしかない. いずれにしても原点を中心とした回転を考えることになるため, 中心が原点でない場合,\ 一旦中心が原点となるよう平行移動する必要がある. 複素数平面を利用し,\ 関数を原点を中心として\ ${θ}$\ 回転させることを考える. $(X,\ Y)を(x,\ y)で表した後,\ (x,\ y)を(X,\ Y)に表し直すのは面倒である.$ そこで,\ $(X,\ Y)}を-θ\ 回転すると,\ (x,\ y)}に戻ると考えて立式する.$ $-θ\ 回転を表す複素数は,\ cos(-θ)+isin(-θ)=cosθ-isinθ\ であるから,$ 行列を利用し,\ 関数を原点を中心として\ ${θ}$\ 回転させることを考える. 原点を中心とする\ $θ\ の回転を表す行列は \gyouretu[r]{cosθ}{-sinθ}{sinθ}{cosθ}$ $(X,\ Y)を(x,\ y)で表した後,\ (x,\ y)を(X,\ Y)に表し直すのは面倒である.$ そこで,\ $(X,\ Y)}を\ -θ\ 回転すると,\ (x,\ y)}に戻ると考えて立式する.$ $-θ\ 回転を表す行列は 実際に,\ $回転移動の例として,\ y=x²\ を原点を中心に-90° 回転させてみる.$ 複素数平面と行列のどちらも,\ 実質は三角関数の加法定理である. また,\ そもそも加法定理は,\ 図形的には回転を意味している. つまり,\ 複素数平面か行列なしで回転移動するには,\ 加法定理を利用できる. 0.98}{まず,\ $移動前の点を(x,\ y)=(rcosα,\ rsinα)}\ のように距離rと角\ α\ で表す.$}

