平行移動において関数の移動を理解しておくと、対称移動や回転移動などあらゆる移動が同様の原理で可能であることに気付く。
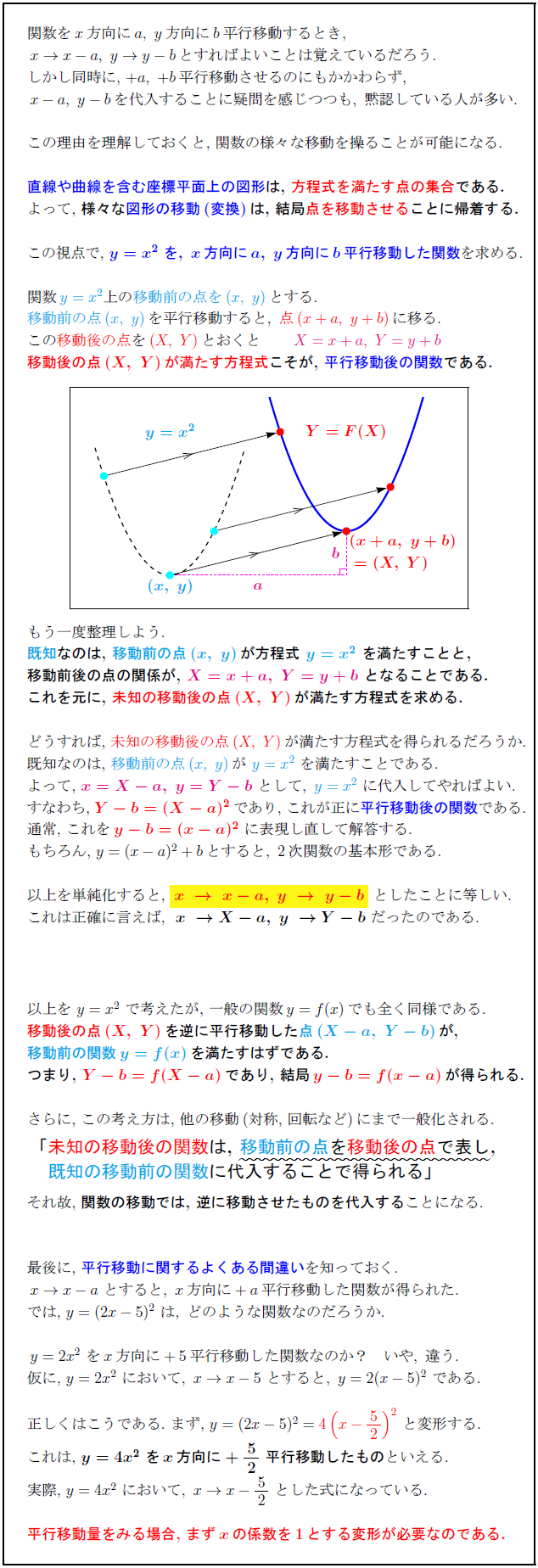
関数を$x方向にa,\ y方向にb$平行移動するとき, $x→ x-a,\ y→ y-b$とすればよいことは覚えているだろう. しかし同時に,\ $+a,\ +b$平行移動させるのにもかかわらず, $x-a,\ y-bを代入することに疑問を感じつつも,\ 黙認している人が多い.$ この理由を理解しておくと,\ 関数の様々な移動を操ることが可能になる. 直線や曲線を含む座標平面上の図形}は,\ 方程式を満たす点の集合}である.} よって,\ 様々な図形の移動(変換)}は,\ 結局点を移動させる}ことに帰着する.} 0.98}{この視点で,\ ${y=x²\ を,\ x方向にa,\ y方向にb平行移動した関数を求める.$} 関数$y=x²}上の移動前の点を(x,\ y)}とする.$ 移動前の点}$(x,\ y)}を平行移動すると,\ 点(x+a,\ y+b)}に移る.$ この移動後の点}を$(X,\ Y)}$とおくと $X=x+a,\ Y=y+b}$ 移動後の点}${(X,\ Y)$が満たす方程式}こそが,\ 平行移動後の関数}である もう一度整理しよう. 既知}なのは,\ 移動前の点}${(x,\ y)}が方程式\ y=x²}\ を満たすことと,}$} 移動前後の点の関係が,\ ${X=x+a,\ Y=y+b}\ となることである.}$} これを元に,\ 未知の移動後の点${(X,\ Y)}$}が満たす方程式を求める.} どうすれば,\ 未知の移動後の点$(X,\ Y)$}が満たす方程式を得られるだろうか. 既知なのは,\ 移動前の点}$(x,\ y)}が\ y=x²}\ を満たすことである.$ よって,\ ${x=X-a,\ y=Y-b\ として,\ y=x²}\ に代入してやればよい.$ すなわち,\ ${Y-b=(X-a)²$であり,\ これが正に平行移動後の関数である. 通常,\ これを${y-b=(x-a)²$\ に表現し直して解答する. もちろん,\ $y=(x-a)²+bとすると,\ 2次関数の基本形である.$ 以上を単純化すると,\ yellow}{${x\ →\ x-a,\ y\ →\ y-b$}\ としたことに等しい. これは正確に言えば,${x\ → X-a,\ y\ → Y-b}\ だったのである$. 以上を\ $y=x²$\ で考えたが,\ 一般の関数$y=f(x)$でも全く同様である. 移動後の点${(X,\ Y)}$}を逆に平行移動}した点${(X-a,\ Y-b)}$}が, 移動前の関数${y=f(x)}$}を満たすはずである. つまり,\ ${Y-b=f(X-a)$であり,\ 結局${y-b=f(x-a)$が得られる.} さらに,\ この考え方は,\ 他の移動(対称,\ 回転など)にまで一般化される. { 「未知の移動後の関数}は,\ \namikasen{移動前の点}を移動後の点}で表し}, 既知の移動前の関数}に代入することで得られる」 それ故,\ 関数の移動では,\ 逆に移動させたものを代入する}ことになる. 最後に,\ 平行移動に関するよくある間違いを知っておく. $x→ x-a\ とすると,\ x方向に+a平行移動した関数が得られた.$ では,\ $y=(2x-5)²\ は,\ どのような関数なのだろうか.$ $y=2x²\ をx方向に+5平行移動した関数なのか? いや,\ 違う.$ 仮に,\ $y=2x²\ において,\ x→ x-5\ とすると,\ y=2(x-5)²\ である.$ 正しくはこうである.\ まず, と変形する.$ これは,\ ${y=4x²\ をx方向に+52\ 平行移動したもの}といえる.$ 実際,\ $y=4x²\ において,\ x→ x-52\ とした式になっている.$ 平行移動量をみる場合,}\ ${まずxの係数を1とする変形が必要なのである.}$}

