関数を見たとき、単なる数式としか見れないのかおおよその概形がイメージができるのかの差は大きい。
特に基本的な分数関数のグラフは、数Ⅲの範囲ではあるが文系でも概形を描けたほうがよい。中学生の時に学習した反比例の式と平行移動を組み合わせただけである。分子の次数を分母より低くする変形法は他で取り上げる。
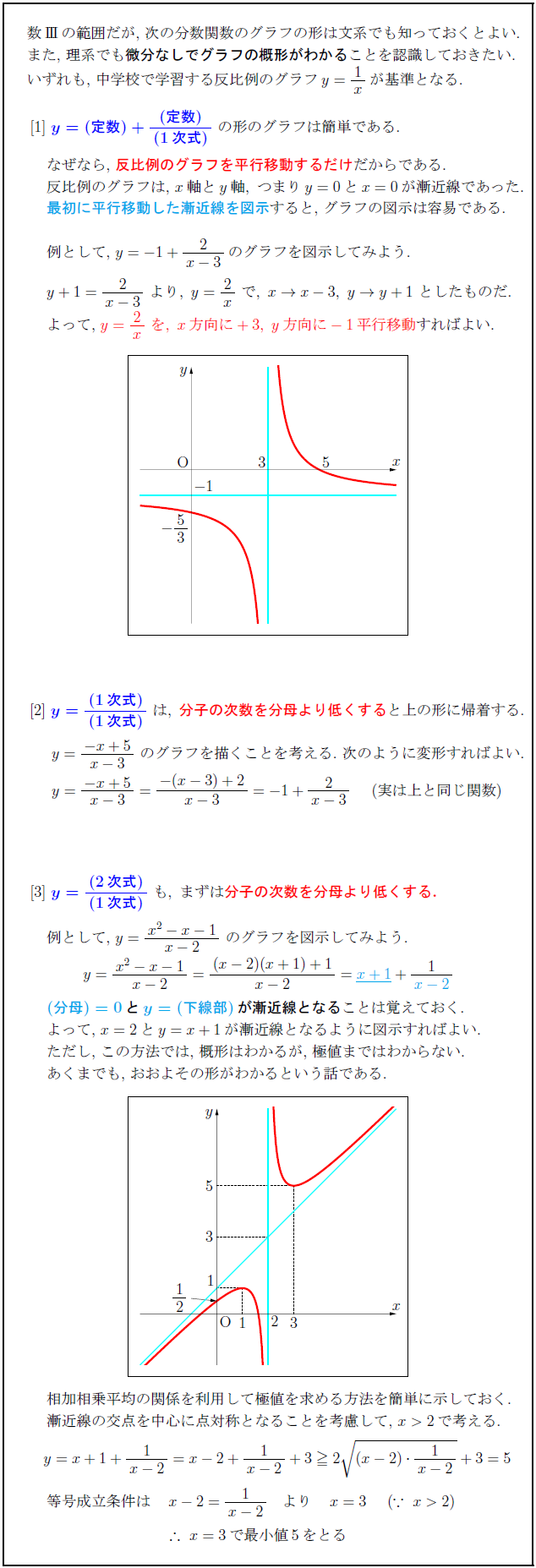
数IIIの範囲だが,\ 次の分数関数のグラフの形は文系でも知っておくとよい. また,\ 理系でも微分なしでグラフの概形がわかる}ことを認識しておきたい. いずれも,\ 中学校で学習する反比例のグラフ$y=1x$が基準となる. $\ {y=(定数)+{(定数)}{(1次式)}\ の形のグラフは簡単である.$ \ なぜなら,\ 反比例のグラフを平行移動するだけだからである. \ 反比例のグラフは,\ $x軸とy軸,\ つまりy=0とx=0$が漸近線であった. \ 最初に平行移動した漸近線を図示すると,\ グラフの図示は容易である. \ 例として,\ $y=-1+{2}{x-3}$のグラフを図示してみよう. \ $y+1={2}{x-3}\ より,\ y=2x\ で,\ x→ x-3,\ y→ y+1\ としたものだ.$ \ よって,\ $y=2x\ を,\ x方向に+3,\ y方向に-1平行移動}すればよい.$ y={(1次式)}{(1次式)}\ は,\ {分子の次数を分母より低くすると上の形に帰着する.$ $y={-x+5}{x-3}\ のグラフを描くことを考える.\ 次のように変形すればよい.$ $y={-x+5}{x-3}={-(x-3)+2}{x-3}=-1+{2}{x-3}$ (実は上と同じ関数) y={(2次式)}{(1次式)}\ も,\ まずは{分子の次数を分母より低くする.$ \ 例として,\ $y={x²-x-1}{x-2}$\ のグラフを図示してみよう. \ ${(分母)=0}とy=(下線部)}が漸近線となる}ことは覚えておく.$ \ よって,\ $x=2とy=x+1が漸近線となるように図示すればよい.$ \ ただし,\ この方法では,\ 概形はわかるが,\ 極値まではわからない. \ あくまでも,\ おおよその形がわかるという話である. \ 相加相乗平均の関係を利用して極値を求める方法を簡単に示しておく. \ 漸近線の交点を中心に点対称となることを考慮して,\ で考える. \ \ $等号成立条件は x-2={1}{x-2} より x=3 (∵\ )$ \ $ \ x=3で最小値5をとる$

