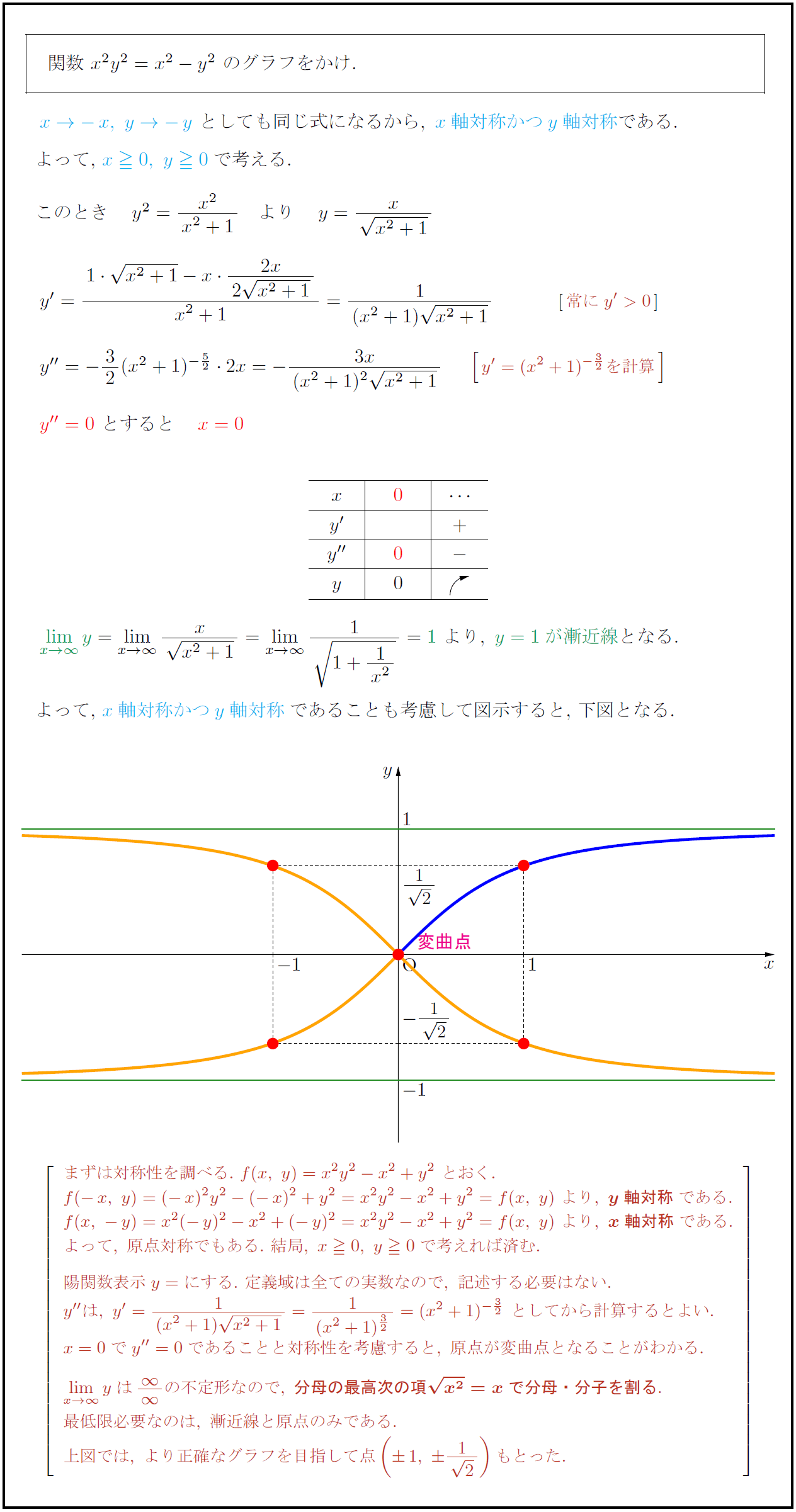
まずは対称性を調べる.\ f(x,\ y)=x²y²-x²+y²\ とおく. f(-x,\ y)=(-x)²y²-(-x)²+y²=x²y²-x²+y²=f(x,\ y)\ より,\ {y軸対称}である. f(x,\ -y)=x²(-y)²-x²+(-y)²=x²y²-x²+y²=f(x,\ y)\ より,\ {x軸対称}である. よって,\ 原点対称でもある.\ 結局,\ x0,\ y0で考えれば済む. 陽関数表示y=にする.\ 定義域は全ての実数なので,\ 記述する必要はない. y”は,\ y’={1}{(x²+1){x²+1={1}{(x²+1)^{3/2=(x²+1)^{-3/2}\ としてから計算するとよい. x=0でy”=0であることと対称性を考慮すると,\ 原点が変曲点となることがわかる. lim[x→∞]yは{∞}{∞}の不定形なので,\ {分母の最高次の項{x²}=xで分母・分子を割る}. 最低限必要なのは,\ 漸近線と原点のみである. 上図では,\ より正確なグラフを目指して点(1,\ {1}{2})もとった.

