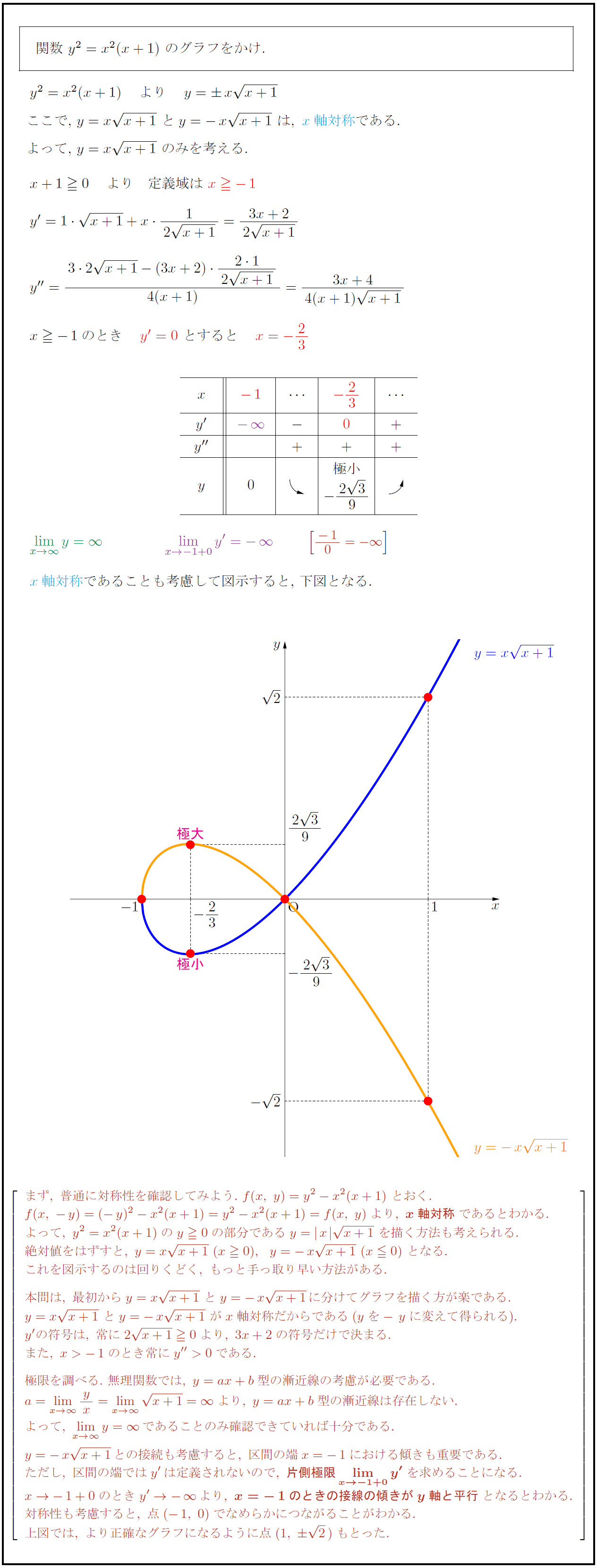
まず,\ 普通に対称性を確認してみよう.\ f(x,\ y)=y²-x²(x+1)\ とおく. f(x,\ -y)=(-y)²-x²(x+1)=y²-x²(x+1)=f(x,\ y)より,\ {x軸対称}であるとわかる. よって,\ y²=x²(x+1)のy0の部分であるy= x{x+1}\ を描く方法も考えられる. 絶対値をはずすと,\ y=x{x+1}\ (x0),y=-x{x+1}\ (x0)\ となる. これを図示するのは回りくどく,\ もっと手っ取り早い方法がある. 本問は,\ 最初からy=x{x+1}\ とy=-x{x+1}に分けてグラフを描く方が楽である. y=x{x+1}\ とy=-x{x+1}\ がx軸対称だからである(yを-yに変えて得られる). y’の符号は,\ 常に2{x+1}0より,\ 3x+2の符号だけで決まる. また,\ x>-1のとき常にy”>0である. 極限を調べる.\ 無理関数では,\ y=ax+b型の漸近線の考慮が必要である. a=lim[x→∞] yx=lim[x→∞]{x+1}=∞ より,\ y=ax+b型の漸近線は存在しない. よって,\ lim[x→∞]y=∞であることのみ確認できていれば十分である. y=-x{x+1}との接続も考慮すると,\ 区間の端x=-1における傾きも重要である. ただし,\ 区間の端ではy’は定義されないので,\ {片側極限limx→-1+0}y’}を求めることになる. x→-1+0のときy’→-∞より,\ {x=-1のときの接線の傾きがy軸と平行}となるとわかる. 対称性も考慮すると,\ 点(-1,\ 0)でなめらかにつながることがわかる. 上図では,\ より正確なグラフになるように点(1,\ 2)もとった.

