問題
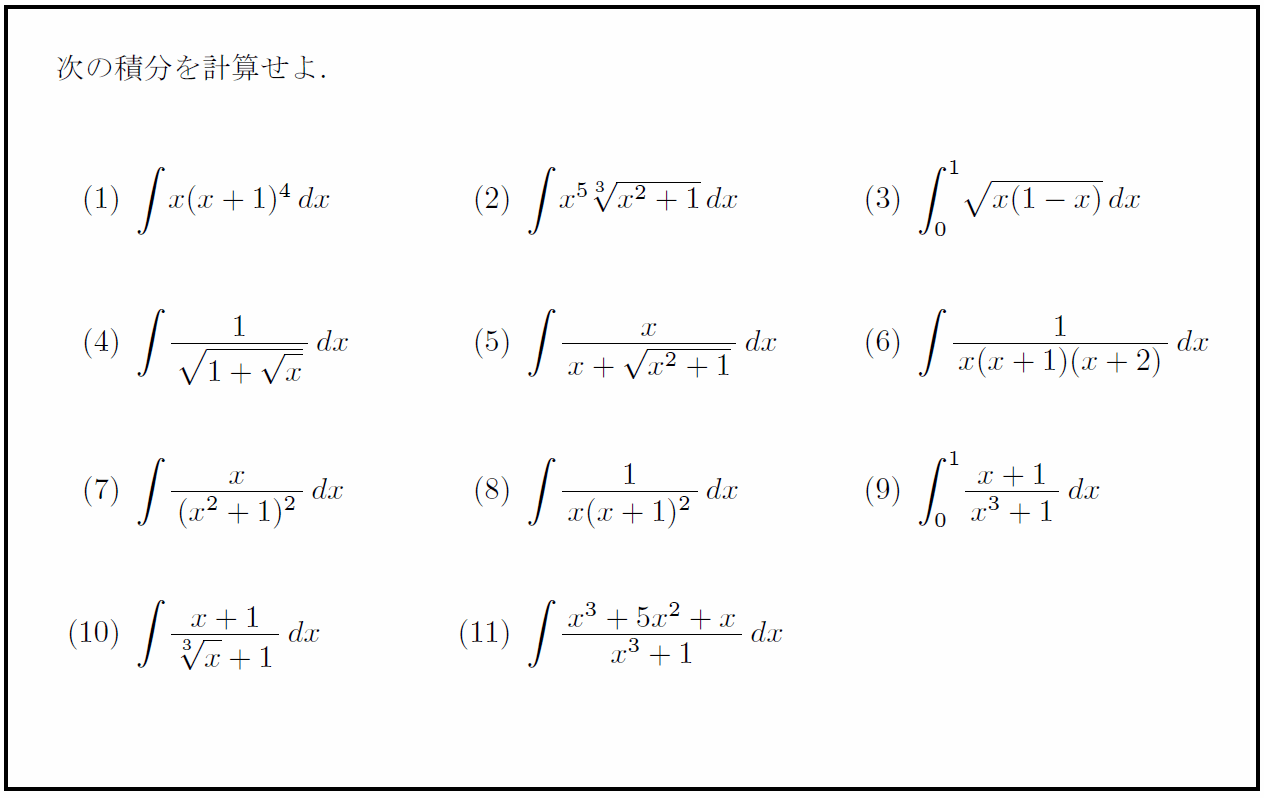
解答
主な解法が3つある.\ 1つ目は部分積分である. 2つ目の置換積分は自然でわかりやすいが,\ 計算量・記述量が増えてしまう. $tからxに戻す前に因数分解しておくこと.$ 3つ目の$x-1$で展開する方法が最も簡潔で推奨される. 一見すると答えが違うが,\ 変形すると一致する. x²)’=2xが接触しているから微分形接触型である.$ $x²+1=t$と置換してもよいが,\ 根号を丸ごと置換すると後で根号の処理をせずに済む. $x²+1=t³\ の両辺をxで微分すると 2x=3t²{dt}{dx}(合成関数の微分)$ の両辺を2乗して整理すると (x-12)²+y²=14(y0)}$ よって,\ 求める定積分は右図の面積(半円)に等しい.{-x²+ax+b}\ 型は,\ 平方完成すると\ {a²-x²}\ 型に帰着する.$ $よって,\ {a²-x²}\ 型と同じく円の面積と見なすべきである.$ ${-x²+ax+b}\ を含む式が常に円を表すとは限らないので,\ 別解も要確認である.$ ${a²-x²}\ 型は,\ x=asinθ\ と置換する.$ $積分区間内では\ cosθ0\ であるから,\ 絶対値ははずすことができる.$ また,\ 積分区間が対称であるから,\ 偶関数・奇関数の可能性を探る. $f(θ)=cos²θ\ とすると\ f(-θ)=cos²(-θ)=cos²θ=f(θ)\ より,\ f(θ)は偶関数である.$ $cos²θ\ は,\ 2倍角の公式\ cos2θ=2cos²θ-1\ の逆を用いて次数を下げる.$ と置換すると二度手間になるので,\ 丸ごと置換する.$ $1+ x=t²\ の両辺をxで微分して 有理化することで分母を定数にできる型である. $x{x²+1}\ は微分形接触累乗型なので,\ x²+1=t\ か\ {x²+1}=t\ と置換して積分できる.$ $微分形接触累乗型\ ∫{f(x)}^{α}f'(x)dx=f(x)}^{α+1{α+1}+C\ とみなすと瞬殺できる.分母をはらうと$ $ 1=A(x+1)(x+2)+Bx(x+2)+Cx(x+1)$ $x=0を代入してA=12,\ x=-1を代入してB=-1,\ x=-2を代入してC=12\ を得る.(x²+1)=2x’$が接触しているから微分形接触型である. さらに,\ 微分形接触累乗型とみなすと瞬殺できる. 分母に累乗の因数がある場合,\ その因数の1次から最高次までを全て分母として分解する. ${1}{x(x+1)²}={A}{x}+{B}{x+1}+{C}{(x+1)²}\ とおいて分母をはらうと$ $ 1=A(x+1)²+Bx(x+1)+Cx$ $x=0としてA=1,x=-1としてC=-1,x=1としてB=-1を得る.$ とりあえず約分できることに気付かなければならない. $(分母の2次式)=0においてD<0ならば,\ 平方完成して\ {1}{x²+a²}\ 型の積分に帰着させる.$ この型は$x=atanθ$と置換する.\ また,\ $1+tan²θ={1}{cos²θ}$\ を適用することになる. と置換してもよいが,\ 約分できることに気付ければ速い.$ $x+1=([3]{x})³+1³\ とみて\ a³+b³=(a+b)(a²-ab+b²)\ を適用する.$ $(分子の次数)(分母の次数)であるから,\ まずは分子の次数を下げるのが先決である.$ $(分子の次数)=(分母の次数)なら,\ 分子に分母と同じ形を作ってつじつまを合わせるとよい.$ 後は部分分数分解だが,\ 分母が2次式の分数は分子が1次以下の式となることに注意する. $5x²+x-1={A}{x+1}+{Bx+C}{x²-x+1}\ とおいて分母をはらうと$ $5x²+x-1=A(x²-x+1)+(Bx+C)(x+1)$ $x=-1としてA=1,x=0としてC=-2,x=1としてB=4を得る.$ 結局,\ 分子が分母の微分型に帰着する.

