定期試験レベルの基本問題です。
問題
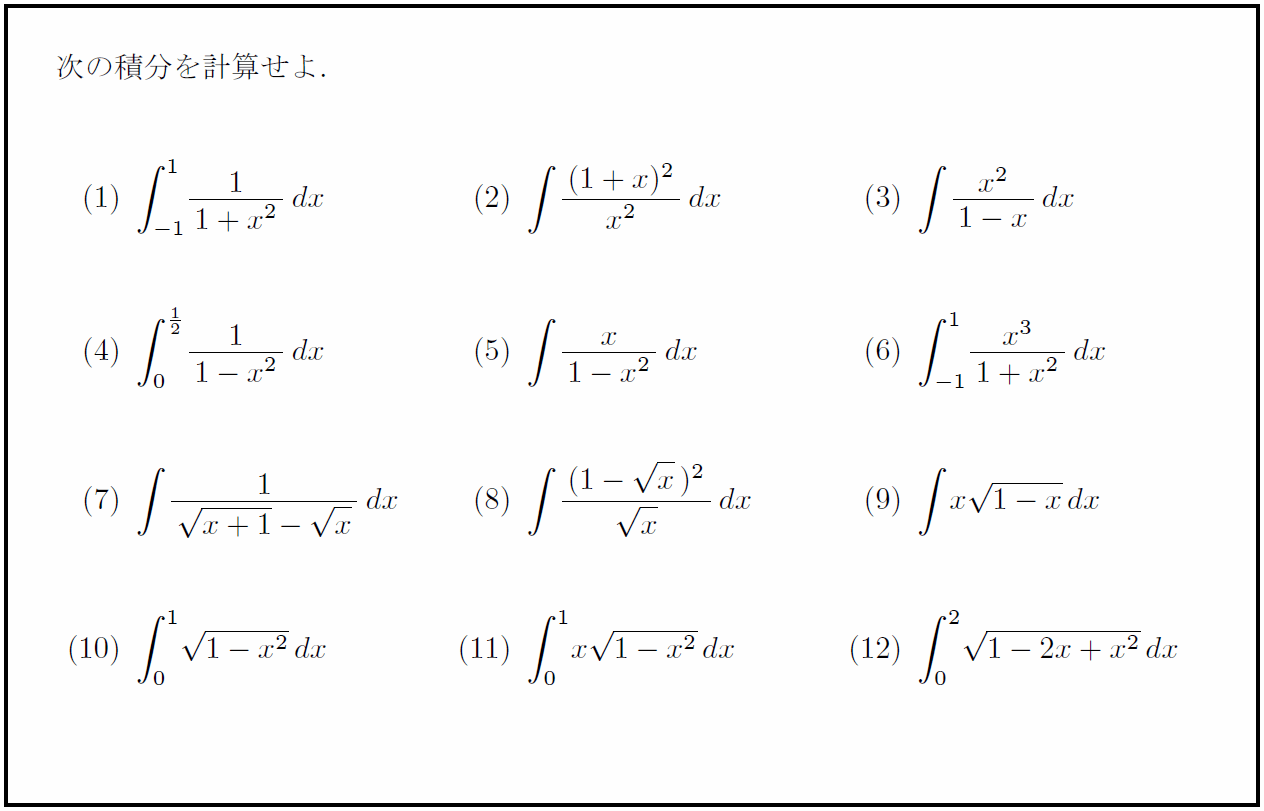
解答
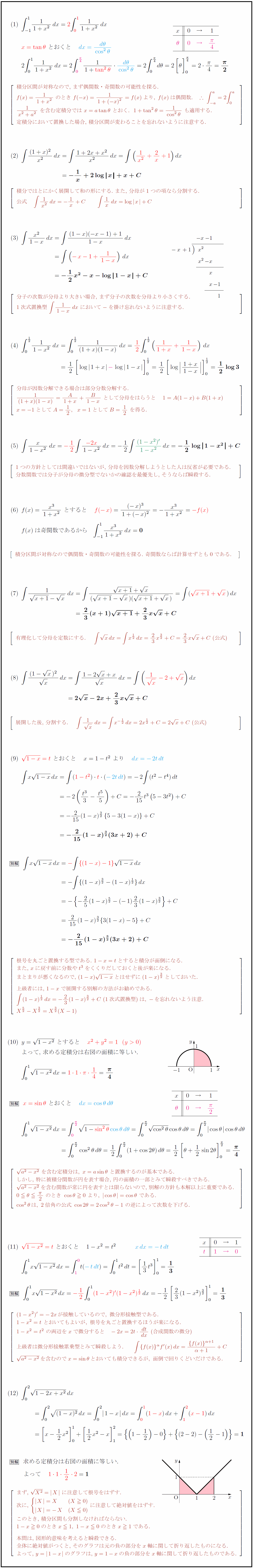
∫1/(1+x²)dx ∫(1+x)²/x²dx ∫x²/(1-x)dx ∫1/(1-x²)dx ∫x/(1-x²)dx ∫x³/(1+x²)dx ∫1/(√(x+1)-√x)dx ∫(1-√x)²/√xdx ∫x√(1-x)dx ∫√(1-x²)dx ∫x√(1-x²)dx ∫√(1-2x+x²)dx 積分区間が対称なので,\ まず偶関数・奇関数の可能性を探る. \ f(x)は偶関数.も適用する.$ 定積分において置換した場合,\ 積分区間が変わることを忘れないように注意する. 積分ではとにかく展開して和の形にする.\ また,\ 分母が1つの項なら分割する. 分子の次数が分母より大きい場合,\ まず分子の次数を分母より小さくする. 1次式置換型\ $∫{1}{1-x}dx$\ において$-$を掛け忘れないように注意する. 分母が因数分解できる場合は部分分数分解する. \ 1つの方針としては間違いではないが,\ 分母を因数分解しようとした人は反省が必要である. 分数関数では分子が分母の微分型でないかの確認を最優先し,\ そうならば瞬殺する. 積分区間が対称なので偶関数・奇関数の可能性を探る.\ 奇関数ならば計算せずとも0である. 有理化して分母を定数にする. (公式 展開した後,\ 分割する. 根号を丸ごと置換する型である.\ $1-x=t$とすると積分が面倒になる. また,\ $x$に戻す前に分数や$t³$をくくりだしておくと後が楽になる. まとまりが悪くなるので,\ $(1-x){1-x}$とはせずに$(1-x)^{3/2}$としておいた. 上級者には,\ $1-x$で展開する別解の方法がお勧めである. $∫(1-x)^{1/2}dx=-23(1-x)^{3/2}+C\ (1次式置換型)は,\ -を忘れないよう注意.$ よって,\ 求める定積分は右図の面積に等しい. ${a²-x²}\ を含む定積分は,\ x=asin θ\ と置換するのが基本である.$ しかし,\ 特に被積分関数が円を表す場合,\ 円の面積の一部とみて瞬殺すべきである. ${a²-x²}$を含む関数が常に円を表すとは限らないので,\ 別解の方針も本解以上に重要である. $0θ{π}{2}\ のとき\ cosθ0\ より,\ cosθ}=cosθ\ である.$ $cos²θは,\ 2倍角の公式\ cos2θ=2cos²θ-1\ の逆によって次数を下げる.$ $(1-x²)’=-2xが接触しているので,\ 微分形接触型である.$ $1-x²=t\ とおいてもよいが,\ 根号を丸ごと置換するほうが楽になる.$ $1-x²=t²\ の両辺をxで微分すると -2x=2t{dt}{dx}\ (合成関数の微分)$ $上級者は微分形接触累乗型とみて瞬殺しよう. ∫{f(x)}^α f'(x)dx=f(x)}^{α+1{α+1}+C$ ${a²-x²}を含むのでx=sinθとおいても積分できるが,\ 面倒で回りくどいだけである.$ に注意して根号をはずす.$ \ $に注意して絶対値をはずす. ₀ このとき,\ 積分区間も分割しなければならない. $1-x0のときx1,\ 1-x0のときx1である.$ 本問は,\ 図形的意味を考えると瞬殺できる. 全体に絶対値がつくと,\ そのグラフは元の負の部分を$x$軸に関して折り返したものになる. よって,\ $y=1-x}$のグラフは,\ $y=1-x$の負の部分を$x$軸に関して折り返したものである.

