定期試験レベルの基本問題です。
問題
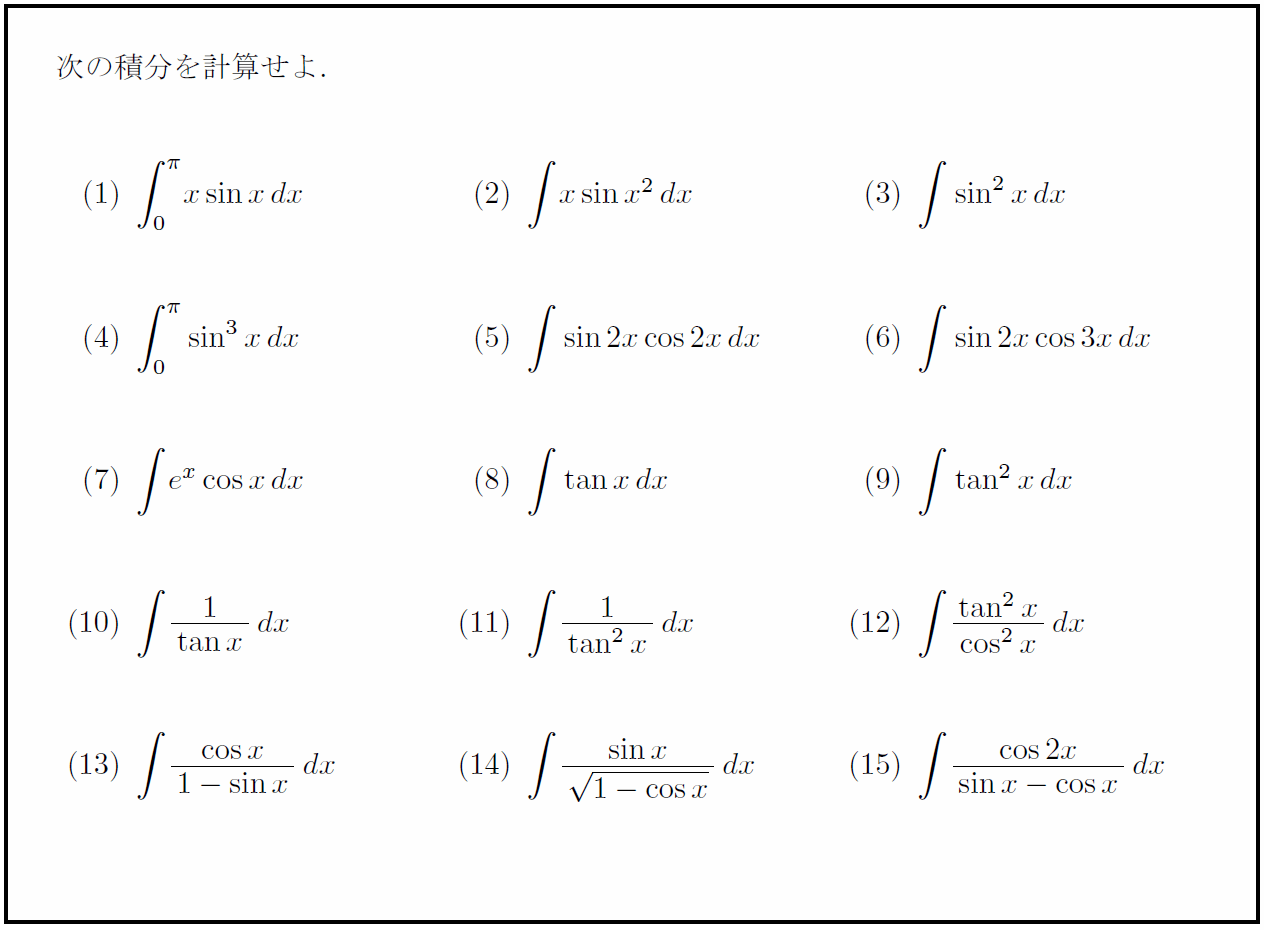
解答

x^msin nx型は,\ sin nxを微分形と見て部分積分する.$ $(x²)’=2xが接触しているので,\ 微分形接触型である.\ x²=tとし,\ 置換積分する.$ $2倍角の公式\ cos2x=1-2sin²x\ の逆で次数を下げる.$ $基本は3倍角の公式\ sin3x=-4sin³x+3sin x\ の逆による次数下げである(本解).$ $sin xを1個分離して残りをcos xで表し,\ 微分形接触型f(cos x)sin xにする別解もある.$ 本問では回りくどくなるが,\ この別解の考え方は$sin⁵x,\ sin^7xなどに応用できる利点がある.$ 定積分において置換した場合,\ 積分区間が変わることを忘れないように注意する. さらに積分区間が対称になるから,\ 偶関数・奇関数の可能性を探る. $f(t)=1-t²\ とすると\ f(-t)=1-(-t)²=1-t²=f(t)\ より,\ f(t)$は偶関数である. 上級者は,\ 微分形接触累乗型\ $∫{f(x)}^α f'(x)dx=f(x)}^{α+1{α+1}+C$\ とみるのもよい(別解2). $2倍角の公式\ sin2x=2sin xcos x\ を逆に用いて次数を下げる.$ $2倍角の公式により,\ sin2xcos2x=2sin xcos x(2cos²x-1)である.$ $これは微分形接触型\ f(cos x)sin x\ なので,\ cos x=t\ と置換して求めることも可能である.$ $しかし,\ この解法は面倒な上にsin4xcos4xなどに対して応用が利かない.$ 積和の公式$cosαsinβ=12{sin(α+β)-sin(α-β)}$を用いて次数を下げる. $最初にcos3xsin2xとしたのは,\ α-β\ が負になることを避けるためである.$ もちろん,\ $sin2xcos3x=12{sin5x+sin(-x)}=12(sin5x-sin x)$と考えてもよい. 2倍角と3倍角の公式より,\ $sin2xcos3x=2sin xcos x(4cos³x-3cos x)$である. $これは微分形接触型\ f(cos x)sin x\ なので,\ cos x=t\ と置換して求めることも可能である.$ しかし,\ この解法は面倒な上に$sin5xcos4x$などに対して応用が利かない. $e^{mx}sin nx,e^{mx}cos nx\ 型は,\ 2回部分積分すると同型が出現することを利用して求める.$ $sin とcos をペアで考え,\ 微分から逆算するうまい別解もある.$ $tan xはとりあえず\ {sin x}{cos x}としてみるのが積分の基本方針の1つである.$ $特に,\ tan x\ と\ {1}{tan x}$\ は,\ 分子が分母の微分型に帰着する. $tan²x\ と\ {1}{tan²x}\ は,\ 相互関係\ 1+tan²x={1}{cos²x},1+{1}{tan²x}={1}{sin²x}\ を利用する.$ すると,\ 公式\ $∫{1}{cos²x}dx=tan x+C,∫{1}{sin²x}dx=-{1}{tan x}+C$\ に帰着する. 微分形接触型\ $f(tan x){1}{cos²x}\ であるから,\ tan x=t\ と置換すると積分できる$. $よく考えると微分形接触累乗型でもあるので,\ 置換せずとも瞬殺できる.$ $なお,\ 本問は\ tan x={sin x}{cos x}$として積分するのは困難である. 積分では,\ $tan x\ とその微分\ {1}{cos²x}$を常にセットで意識しておくことが重要である. 分数の積分では常にこの確認が最優先である.\ 気付けなかった人は思考順序を改めよう. また,\ $常に\ 1-sin x>0\ なので絶対値はつけない(問題より,\ 分母1-sin x0は確定).$ 微分形接触型である.\ 定数項もまとめて置換する.\ 根号丸ごと置換するのもよい. $1-cos x=t²\ の両辺をxで微分すると sin x=2t{dt}{dx}$(合成関数の微分) $∫{1}{ x}dx=2 x+C$\ は公式として覚えておきたい. $cos2xは2倍角の公式を用いると\ sin xcos x\ と約分できる.

