問題
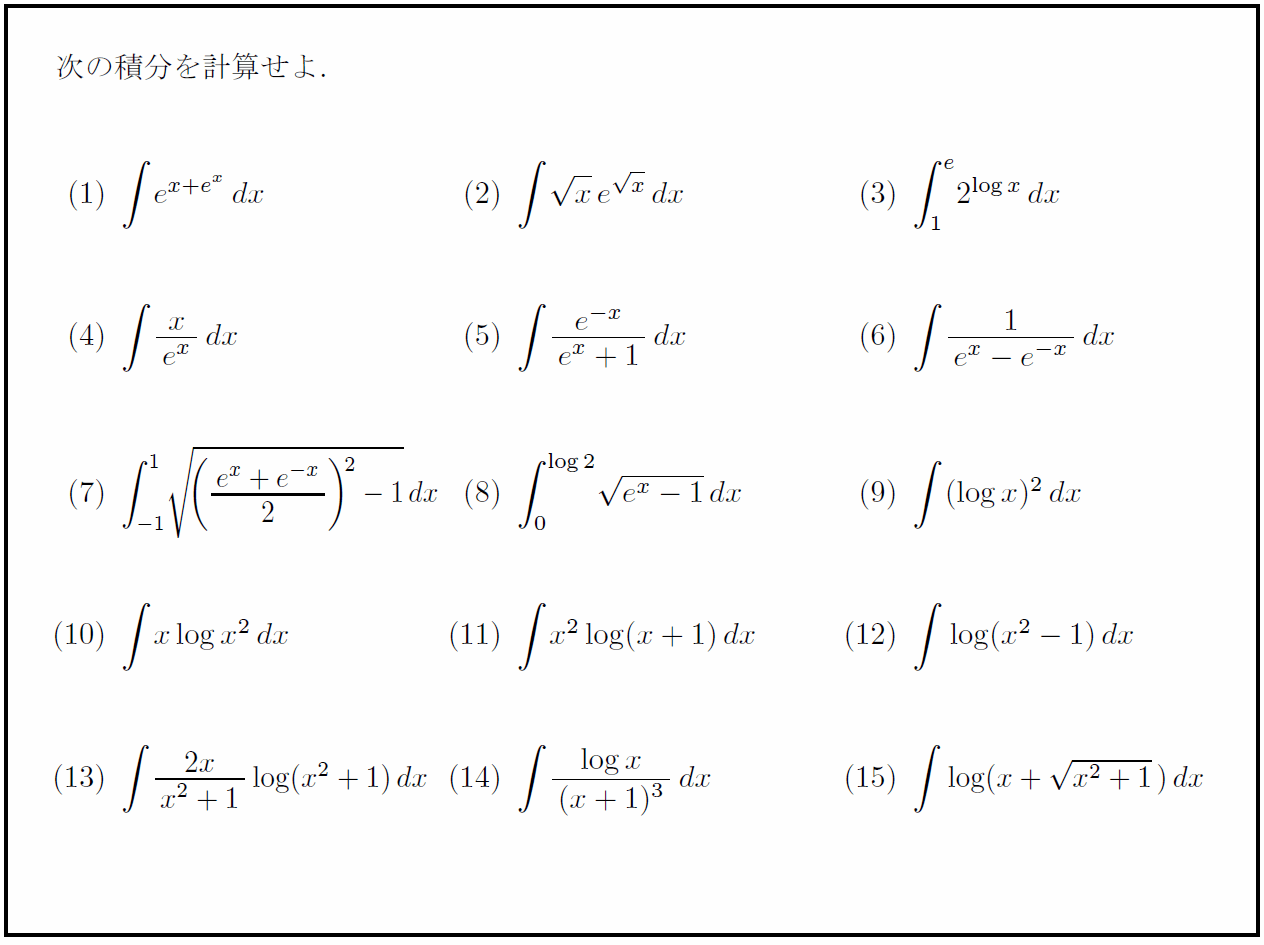
解答

微分形接触型\ $特定の型というわけではないが,\ とりあえず\ x=t\ と置換してみたくなるはずである.$ $x^me^{nx}型に帰着するから,\ 部分積分を2回繰り返す.$ $ちなみに,\ 別解のように置換して求めることもできる. dt\ を求める過程はにあるので省略した.$ $特定の型というわけではないが,\ とりあえず\ log x=t\ と置換してみたくなるはずである.$ $eは定数であるから,\ 2^te^tは2^t3^t=6^tと同じ扱いで積分できる. -x}\ とみなすとx^me^{nx}型であるから,\ 部分積分する. $e^x\ のみの式は,\ e^x=t\ と置換するとtのみの積分に帰着する.$ ${1}{t²(t+1)}= At+{B}{t²}+{C}{t+1}\ として分母をはらうと 1=At(t+1)+B(t+1)+Ct²$ $t=0としてB=1,t=-1としてC=1,t=1としてA=-1\ を得る.$ $常にe^x>0であるから,\ 絶対値ははずせる.$ $分子を分母と同じ形や微分形で表し,\ 分子が分母の微分型に帰着させられれば速い(別解1).$ $分子にe^{-x}があることを考慮すると,\ e^{-x}=tと置換するほうが楽である(別解2).$ おいて分母をはらうと 1=A(t+1)+B(t-1)$ $t=1としてA=12,t=-1としてB=-12\ を得る.$ 中身を以下のように変形することで根号をはずすことができる有名な式である. 根号をはずすとき,\ ${X²}= X$\ であることに注意する. $f(x)は偶関数であるから,\ ∫-1}{1}=2∫\ とできる.\ $り,\ 絶対値はそのままはずせる.$ 偶関数を利用していなければ,\ 絶対値をはずすときに積分区間を分割する羽目になる. $対数の定義\ a^p=Mp=log_aM\ より\ a^{log_aM}=M\ であるから e^{log2}=2$ ${t²}{t²+1}={(t²+1)-1}{t²+1}=1-{1}{t²+1} (分子の次数下げ)$ ${1}{x²+a²}\ を含む定積分では\ x=atanθ\ と置換する.$ $log 単独の積分は,\ log x=1log x=(x)’log xと考えて部分積分する.$ $公式∫log xdx=xlog x-x+Cを覚えておけば1回の部分積分で済む.$ $(x²)’=2xが接触しているので,\ 微分形接触型である.$ $対数の性質\ log M^k=klog M\ を適用した後,\ 部分積分してもよい(別解).$ $ここで,\ log x²=2log x\ ではない.\ 問題がlog x²なので,\ x²>0は確定している.$ $しかし,\ x²>0はx<0,\ 00とは限らないのでlog xとする必要がある.$ $log xを含む場合,\ 部分積分すると(log x)’=1x\ となって絶対値は消える.$ $部分積分における約分を見越し,\ x²={13(x³+1)}’\ とみなすと楽になる.$ $x³+1=(x+1)(x²-x+1)$ 普通に部分積分すると別解のように分子の次数下げが必要になる. $筆算での割り算により 細かく分けると複数の解法が考えられるが,\ いずれにしても部分積分することになる. 部分積分では,\ $1=(x+1)’\ または1=(x-1)’\ とみなすと後が楽になる.$ $x²-1=(x+1)(x-1)\ と約分できるからである.$ 普通に部分積分すると別解1のように分子の次数下げと部分分数分解が必要になる. ${x²}{x²-1}={(x²-1)+1}{x²-1}=1+{1}{x²-1}$ $別解2は,\ 対数の性質\ log MN=log M+log N\ を利用するものである.$ $ここで,\ log(x+1)(x-1)=log(x+1)+log(x-1)\ ではない.$ $問題がlog(x²-1)なので,\ x²-1>0は確定している.$ $しかし,\ x²-1>0はx<-1,\ 10,\ x-1>0とは限らない.$ よって,\ 絶対値をつける必要がある.\ 部分積分における微分で絶対値は消える. $∫log xdx\ に公式\ ∫log xdx=xlog x-x+C\ は適用できないので注意.$ $(x²+1)’=2x\ が接触しているから,\ 微分形接触型である.$ $置換すると,\ (log t)’=1t\ より再び微分形接触型となる.$ $よって,\ log t=uと置換してもよいが,\ 微分形接触累乗型とみると置換せずに済む.$ $実は,\ {log(x²+1)}’={2x}{x²+1}\ が接触しているとみなせれば速い(別解).$ $x^m(log x)^n型のm=-3の場合であるから,\ 部分積分する.$ ${1}{x(x+1)²}={A}{x}+{B}{x+1}+{C}{(x+1)²}\ とおいて分母をはらうと$ \ {微分形接触型}である.\ x²+1=tとしてもよいが,\ 丸ごと置換するとよい.

