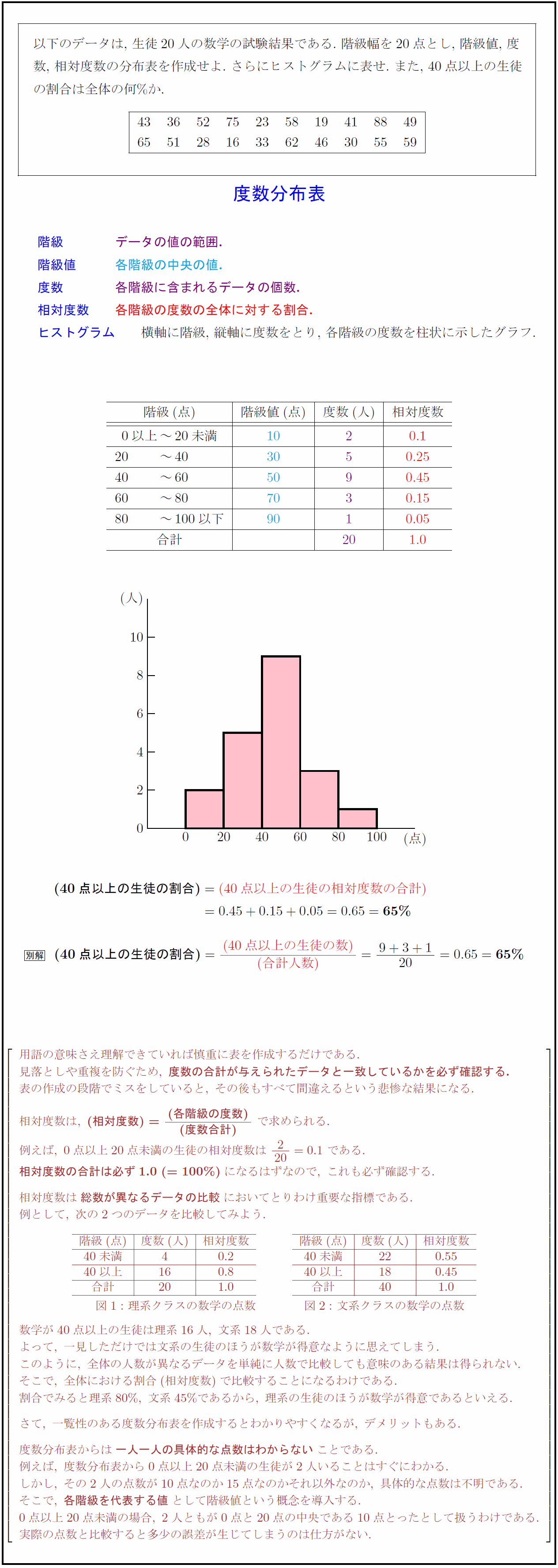
以下のデータは,\ 生徒20人の数学の試験結果である.\ 階級幅を20点とし,\ 階級値,\ 度
数,\ 相対度数の分布表を作成せよ.\ さらにヒストグラムに表せ.\ また,\ 40点以上の生徒
の割合は全体の何\%か.
階級 データの値の範囲.
階級値 各階級の中央の値.
度数 各階級に含まれるデータの個数.
相対度数 各階級の度数の全体に対する割合.
ヒストグラム 横軸に階級,\ 縦軸に度数をとり,\ 各階級の度数を柱状に示したグラフ.
階級(点) & 階級値(点) 度数(人) 相対度数
${(40点以上の生徒の割合)}=(40点以上の生徒の相対度数の合計)}$
$(40点以上の生徒の割合)=0.45+0.15+0.05=0.65={65\%}$
{(40点以上の生徒の割合)}={(40点以上の生徒の数)}{(合計人数)={9+3+1}{20}=0.65={65\%}
用語の意味さえ理解できていれば慎重に表を作成するだけである.
見落としや重複を防ぐため,\ {度数の合計が与えられたデータと一致しているかを必ず確認する.}
表の作成の段階でミスをしていると,\ その後もすべて間違えるという悲惨な結果になる.
相対度数は,\ {(相対度数)={(各階級の度数)}{(度数合計)\ で求められる.
例えば,\ 0点以上20点未満の生徒の相対度数は\ {2}{20}=0.1\ である.
{相対度数の合計は必ず1.0\ (=100\%)}になるはずなので,\ これも必ず確認する.
相対度数は{総数が異なるデータの比較}においてとりわけ重要な指標である.
例として,\ 次の2つのデータを比較してみよう.
図1:理系クラスの数学の点数図2:文系クラスの数学の点数
数学が40点以上の生徒は理系16人,\ 文系18人である.
よって,\ 一見しただけでは文系の生徒のほうが数学が得意なように思えてしまう.
このように,\ 全体の人数が異なるデータを単純に人数で比較しても意味のある結果は得られない.
そこで,\ 全体における割合(相対度数)で比較することになるわけである.
割合でみると理系80\%,\ 文系45\%であるから,\ 理系の生徒のほうが数学が得意であるといえる.
さて,\ 一覧性のある度数分布表を作成するとわかりやすくなるが,\ デメリットもある.
度数分布表からは{一人一人の具体的な点数はわからない}ことである.
例えば,\ 度数分布表から0点以上20点未満の生徒が2人いることはすぐにわかる.
しかし,\ その2人の点数が10点なのか15点なのかそれ以外なのか,\ 具体的な点数は不明である.
そこで,\ {各階級を代表する値}として階級値という概念を導入する.
0点以上20点未満の場合,\ 2人ともが0点と20点の中央である10点とったとして扱うわけである.
実際の点数と比較すると多少の誤差が生じてしまうのは仕方がない.
数,\ 相対度数の分布表を作成せよ.\ さらにヒストグラムに表せ.\ また,\ 40点以上の生徒
の割合は全体の何\%か.
階級 データの値の範囲.
階級値 各階級の中央の値.
度数 各階級に含まれるデータの個数.
相対度数 各階級の度数の全体に対する割合.
ヒストグラム 横軸に階級,\ 縦軸に度数をとり,\ 各階級の度数を柱状に示したグラフ.
階級(点) & 階級値(点) 度数(人) 相対度数
${(40点以上の生徒の割合)}=(40点以上の生徒の相対度数の合計)}$
$(40点以上の生徒の割合)=0.45+0.15+0.05=0.65={65\%}$
{(40点以上の生徒の割合)}={(40点以上の生徒の数)}{(合計人数)={9+3+1}{20}=0.65={65\%}
用語の意味さえ理解できていれば慎重に表を作成するだけである.
見落としや重複を防ぐため,\ {度数の合計が与えられたデータと一致しているかを必ず確認する.}
表の作成の段階でミスをしていると,\ その後もすべて間違えるという悲惨な結果になる.
相対度数は,\ {(相対度数)={(各階級の度数)}{(度数合計)\ で求められる.
例えば,\ 0点以上20点未満の生徒の相対度数は\ {2}{20}=0.1\ である.
{相対度数の合計は必ず1.0\ (=100\%)}になるはずなので,\ これも必ず確認する.
相対度数は{総数が異なるデータの比較}においてとりわけ重要な指標である.
例として,\ 次の2つのデータを比較してみよう.
図1:理系クラスの数学の点数図2:文系クラスの数学の点数
数学が40点以上の生徒は理系16人,\ 文系18人である.
よって,\ 一見しただけでは文系の生徒のほうが数学が得意なように思えてしまう.
このように,\ 全体の人数が異なるデータを単純に人数で比較しても意味のある結果は得られない.
そこで,\ 全体における割合(相対度数)で比較することになるわけである.
割合でみると理系80\%,\ 文系45\%であるから,\ 理系の生徒のほうが数学が得意であるといえる.
さて,\ 一覧性のある度数分布表を作成するとわかりやすくなるが,\ デメリットもある.
度数分布表からは{一人一人の具体的な点数はわからない}ことである.
例えば,\ 度数分布表から0点以上20点未満の生徒が2人いることはすぐにわかる.
しかし,\ その2人の点数が10点なのか15点なのかそれ以外なのか,\ 具体的な点数は不明である.
そこで,\ {各階級を代表する値}として階級値という概念を導入する.
0点以上20点未満の場合,\ 2人ともが0点と20点の中央である10点とったとして扱うわけである.
実際の点数と比較すると多少の誤差が生じてしまうのは仕方がない.

