始めに
もし、895+999のような計算が1秒でできないのであれば、それは計算力が低いからではない。単に、正しい“見方”と“処理方法”を知らないだけである。
世の中には、数字の並びを見た瞬間に計算が終わる――そんな強力な計算技巧がいくつも存在する。それにもかかわらず、学校ではなぜか体系的に教わらない。小学校低学年にはまだ早いかもしれないが、中学生以上ならば、これらの技法はもはや「常識」になってほしい。
数学の試験では、最終的に計算スピードこそが得点力に直結する。速算術は、単に計算そのものを短縮する効果だけでなく、筆算を書く必要がなくなることで圧倒的な時間短縮をもたらす。複雑な計算を避け、手を動かす回数を減らせば、計算ミスも減る。受験はもちろん、日常生活の中でも役立つ“実戦的な技能”である。
ただし、ここで大切なのは、すべての速算技巧を使いこなそうとする必要はまったく無いということ。
人には得意・不得意があるし、頭の中でイメージしやすい計算型は人によって違う。だから、紹介しているすべてを覚えようとするよりも、自分が「これなら使えそう」と思えたものだけを武器にすれば十分である。むしろ、その“使えるものだけを確実に使う”ほうが実戦では強い。
とはいえ、速算術は「方法を知っている」だけでは武器にならない。実戦で確実に使うには、日頃から意識して使い続ける必要がある。慣れてくれば、複数の技巧を場面に応じて組み合わせることもできるようになる。
このカテゴリでは、原理の説明はあえて簡略化している。特に掛け算の速算の多くは展開・因数分解に基づくため、中学校レベルの数学が終わった頃に「なぜできるのか」を考えてみるのも良いだろう。
★は、定期試験や入試で役立つ度、習得のしやすさなどを総合的に評価したものである。
暗記すべき計算
あまりにもよく登場する計算は、速算以前に暗記しておくことが望ましい。
暗記に勝る速算は存在しないことを肝に銘じておいてほしい。
頻出2乗計算 ★★★★★
16までの2乗は非常に良く出くわす。
また、11と15については後に示す他の速算術により、暗記とほぼ変わらない速さで求めることが可能である。

頻出累乗計算 ★★★★
累乗の値は、場合の数・確率(数A)や指数・対数(数Ⅱ)で頻繁に登場する。特に、2の累乗の頻出度合いは半端ではない。

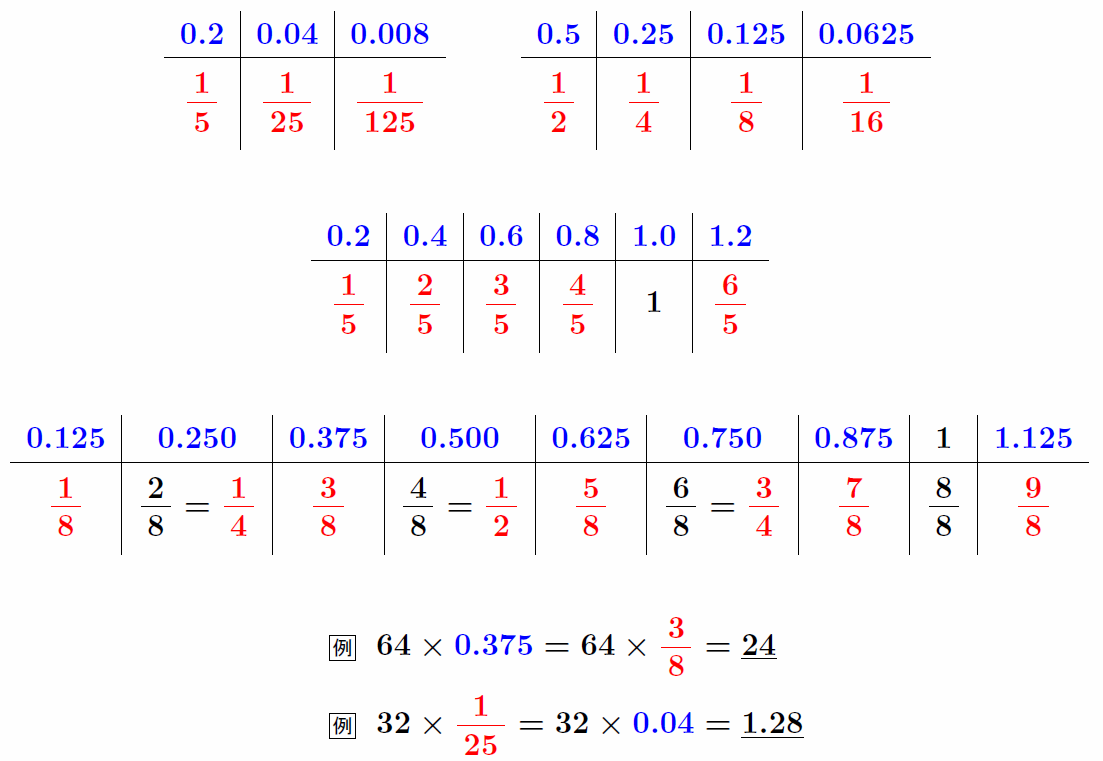
頻出の小数と分数の相互変換 ★★
小数のほうが計算しやすい場合と分数のほうが計算しやすい場合があるため、小数→分数、分数→小数の双方向ができるとよい。
主に分数を利用する数学より、主に小数を利用する理科で利用できることが多い。
足し算の裏技
足し算は引き算で考えよ ★★★★
キリのいい数を足した後で引いて調整することで、繰り上げが多くて鬱陶しい計算を瞬殺できる。
+99を見たとき、「面倒くさい~」ではなく「ラッキー♪」と思えるようになろう。
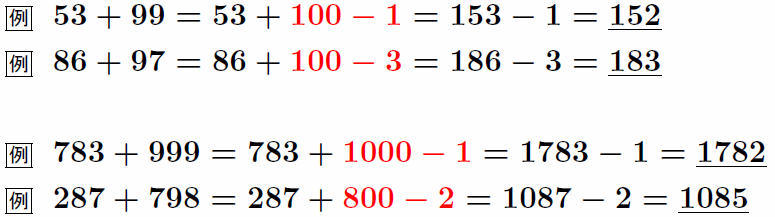
複数の数の足し算の速算 ★★★
和がキリのいい数になる組み合わせを先に計算する。
うまい組み合わせがない場合、キリのいい数を利用するとよい。
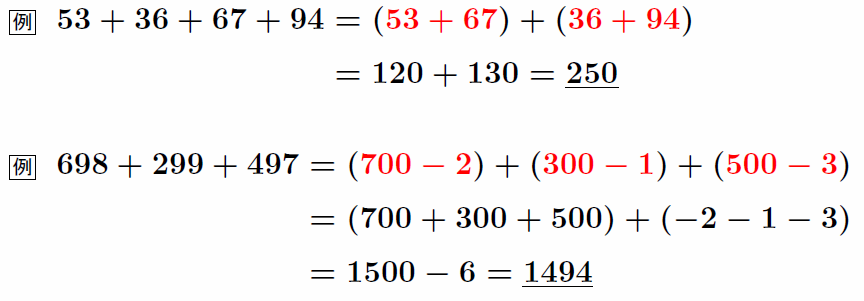
複数の近い数の足し算の速算と仮平均を利用した平均値 ★
近い値が複数ある場合、1つ基準を作り、そこからの誤差を考えて計算する。
この技巧は、平均値を求めるときによく使う手法である。近い値の平均値を求めるときは、仮平均を設定し、そこからの誤差の平均を考えるとよい。

引き算の裏技
引き算は足し算で考えよ ★★★★
キリのいい数を引いた後で足して調整することで繰り下げる必要がなくなる。

1000=999+1と考えよ ★★★★
キリのいい数から引く場合、このように考えると繰り下げる必要がなくなる。
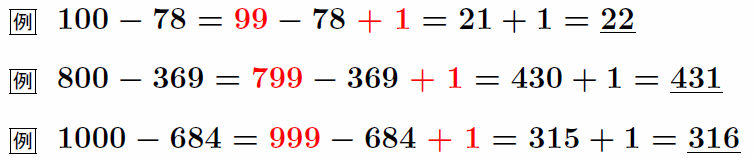
掛け算の裏技
足し算や引き算の速算は、元々計算力が高い人にとってはそこまでの有り難みはない。
しかし、掛け算の速算は通常の数倍の速度で計算が可能になる。掛け算こそ速算術が最も威力を発揮する演算である。
(偶数)×(5の倍数)、(4の倍数)×25、(8の倍数)×125の速算 ★★★★★
利用機会ダントツNo.1の速算術。習得が容易で速算効果も絶大である。

キリのいい数に分解して展開せよ ★★★
掛け算を引き算に変換できる。
特に×99の場合は、下2桁は100との差、上2桁は(元の数)ー1となる。
速算効果が大きく、広く応用が可能だが、実戦で有効な状況はあまり出くわさない。

暗記した累乗を利用せよ ★★

○△×11の速算 ★★★★
筆算する場合を考えると当然のことだが、知っていると筆算する必要がない分時間短縮出来る。

○1×△1、 ○1²の速算 ★★★

○5²の速算 ★★★★★
利用機会がかなり多い。容易なので習得必須。

十の位が等しく、一の位の和が10(十等一和)の速算 ★★
○5²の速算を一般化したものである。
実戦で出くわすことはほぼない。

十の位の和が10で一の位が等しい(十和一等)、5○²の速算 ★
実戦で出くわすことはほぼない。

展開公式(A+B)(A-B)=A²-B² を利用せよ ★★
2数が近く、一の位の和が10であることを適用の目安とするとよい。

展開公式を変形した A²=(A+B)(A-B)+B² を利用せよ ★★
特に100に近い数の2乗において圧倒的な威力を発揮する。

○2²の速算 ★
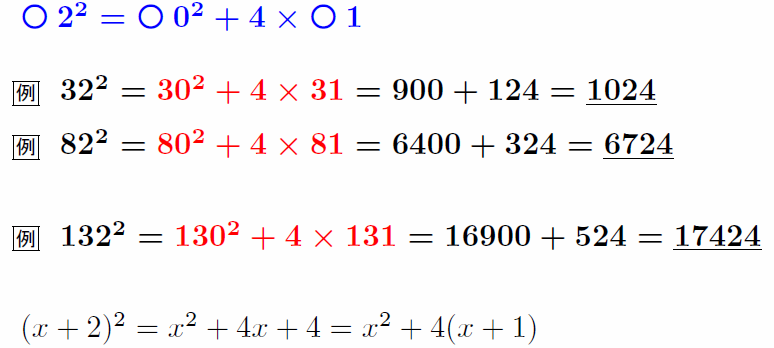
割り算と分数の裏技
割り算は分数で考えよ ★★★★
分数で考えることの利点は約分が出来ることである。割り算の筆算は必要最小限で行う。
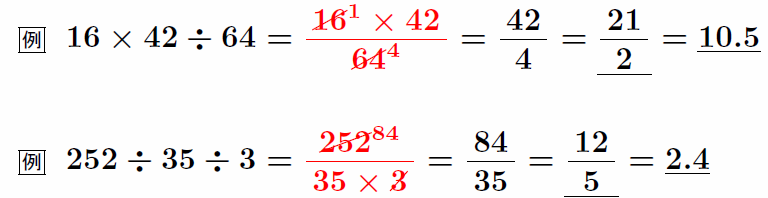
÷5、÷25、÷125は掛け算に変換せよ ★★★
それぞれ2倍、4倍、8倍が10、100、1000というキリのいい数になることを利用する。
また、一般的に割り算よりも掛け算のほうが計算が楽である。

公約数の見つけ方 ★
一見して公約数が見つからない場合でもこの方法ならば確実に見つけることが出来る。
どの素因数でも約分できなければ、その分数は既約である。
この原理は高校数学A:整数で学習する。

倍数条件
倍数条件はそれ自体を問う問題があるが、通常の計算の約分の際に役立てることが重要である。実際に割り算してみる前に、約分できるか否かを判断できる。
また、整数分野(高校数学A)ではこれらの知識は必須事項であり、原理の理解も必要である。
数字の末尾で判別(2、4、8の倍数条件) ★★★★
2の累乗2、4、8の倍数であるための条件は末尾だけで判別できる。その原理も理解しておきたい。
また、割り切れるか否かよりも、余りが一致すると認識しておくと広く応用できる。たとえば、ある数を4で割ったときの余りは、その数の下2桁を4で割ったときの余りと一致する。
ちなみに、同様の原理で5の累乗も末尾で判別可能である。

例題も瞬時に判別できる。
328/532のような分数を見かけたとき、瞬時に4で約分できることがわかるので、2で2回約分するといった無駄な計算を省くことができる。
各桁の和で判別(3、9の倍数条件) ★★★★
こちらも、割り切れるか否かより余りが一致すると認識しておくほうが応用性が広い。たとえば、ある数を3で割ったときの余りは、その数の各位の和を3で割ったときの余りと一致する。

互いに素な2整数の積(6、12、18の倍数条件) ★★★
互いに素な2つの整数両方の倍数であることが条件になる。
なお、互いに素とは2つの整数の最大公約数が1であることを意味する。

上級者用の速算術
元々計算力が高い人・数学的能力が高い人はここで述べる速算術によってさらなる高みを目指すことができる。
理解できる人だけ参考にしてほしい。
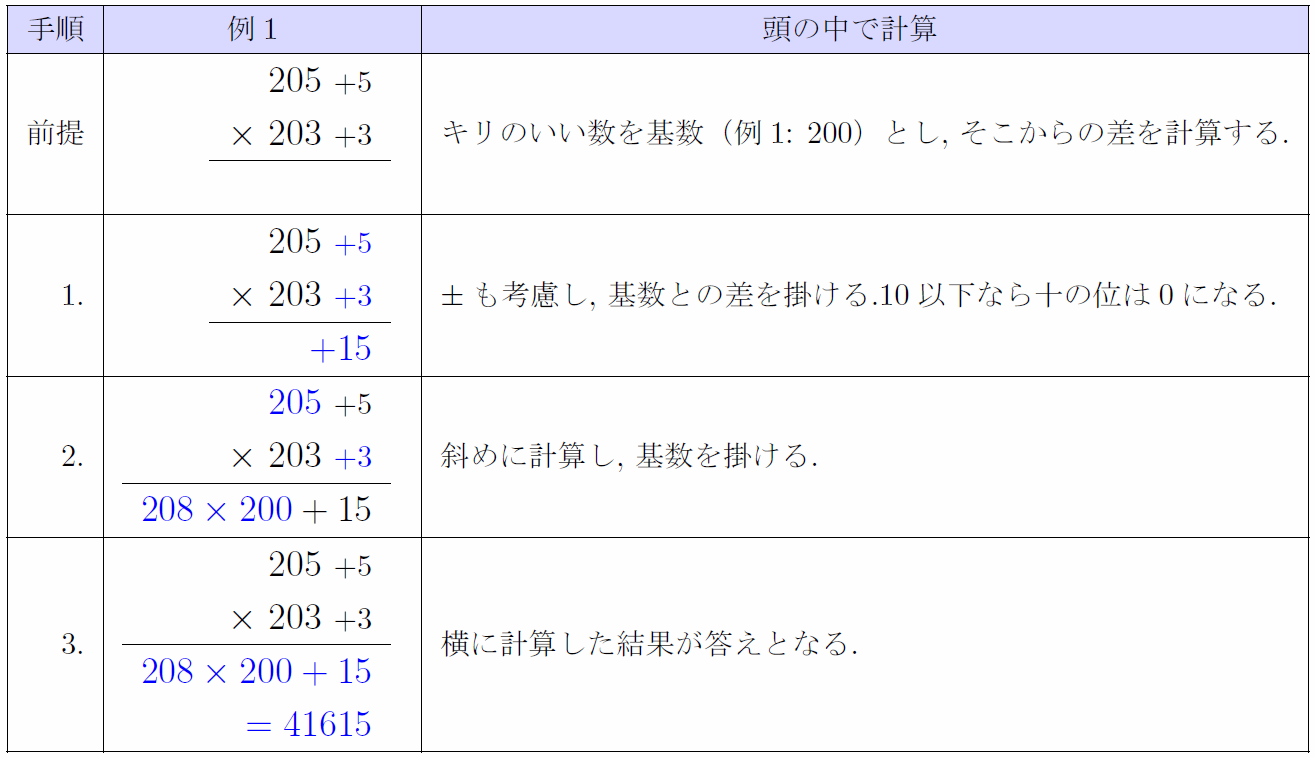
基数を利用した近い2数の掛け算の速算
基準になる数(基数)を決めて、そこからの差を利用すると近い2数の掛け算が簡単に行える。
要は(200+5)(200+3)を計算しているだけ。
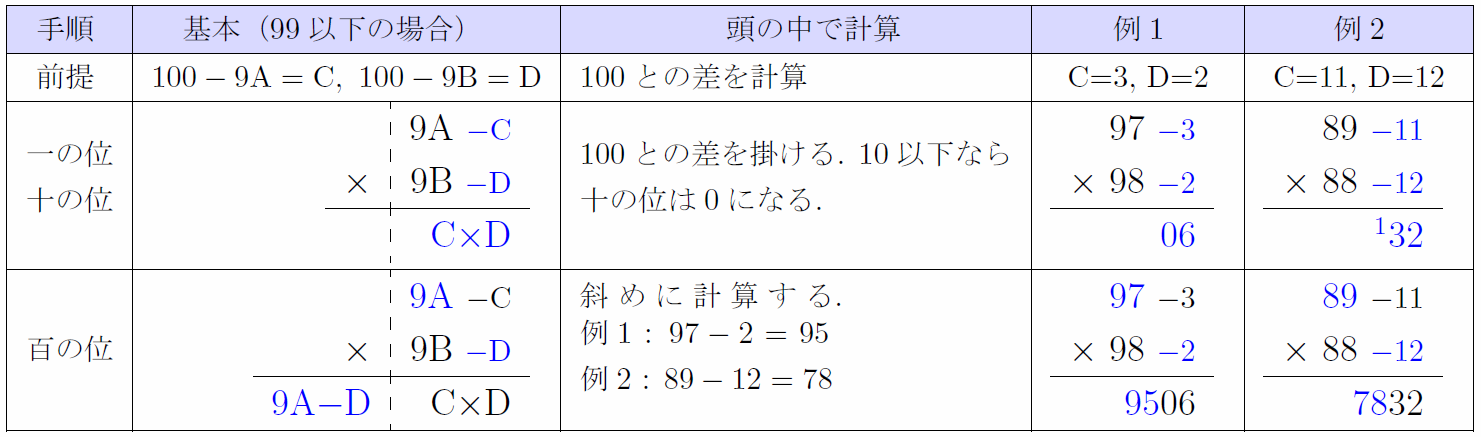
100に近い2数の掛け算の速算
上の基数を利用した方法の特殊な場合である。100に近い2数の掛け算は、基数を100として考えると素早く暗算できる。
要は(100-3)(100-2)を計算しているだけ。
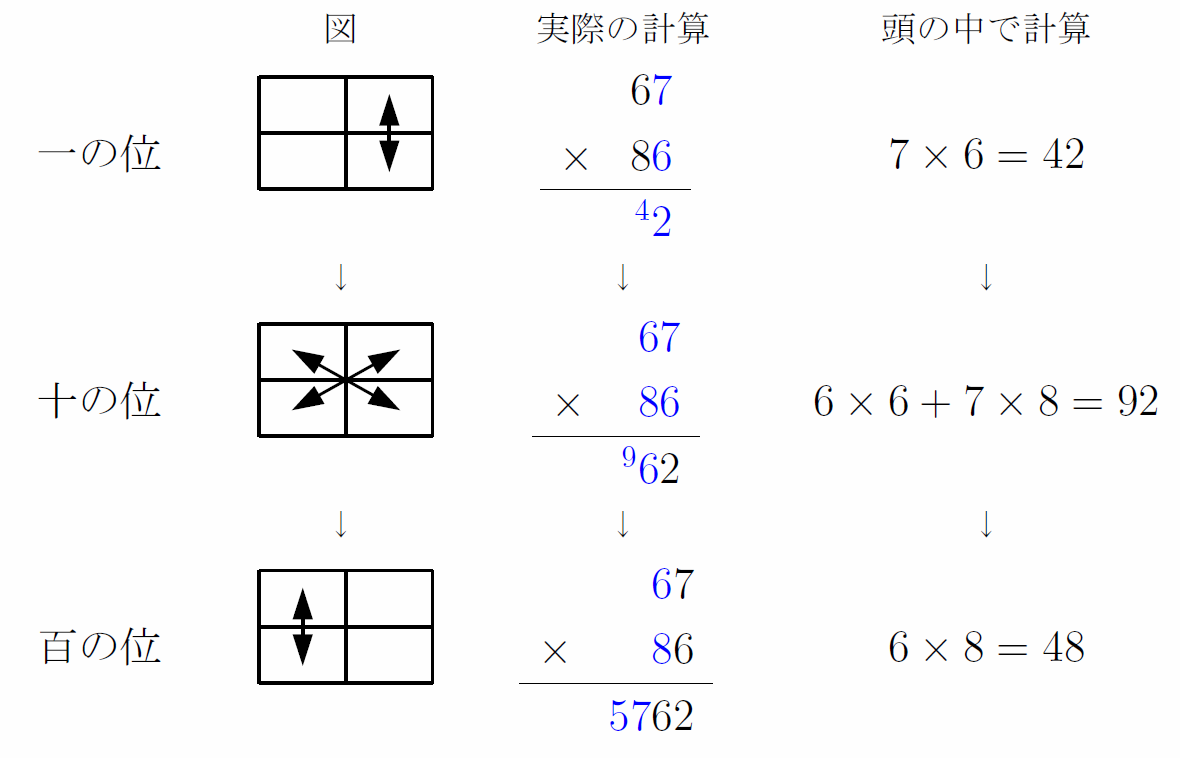
図でわかる2桁×2桁の万能速算術
図のように計算することで、一桁の足し算と掛け算に帰着する。
この方法ならば、ある程度計算力があればいちいち筆算形式に書き直さずに暗算できるようになるだろう。
(ax + b)(cx + d) = acx2 + (ad + bc)x + bd のxに10を代入したと考え、3段階に分けて桁ごとに計算している。
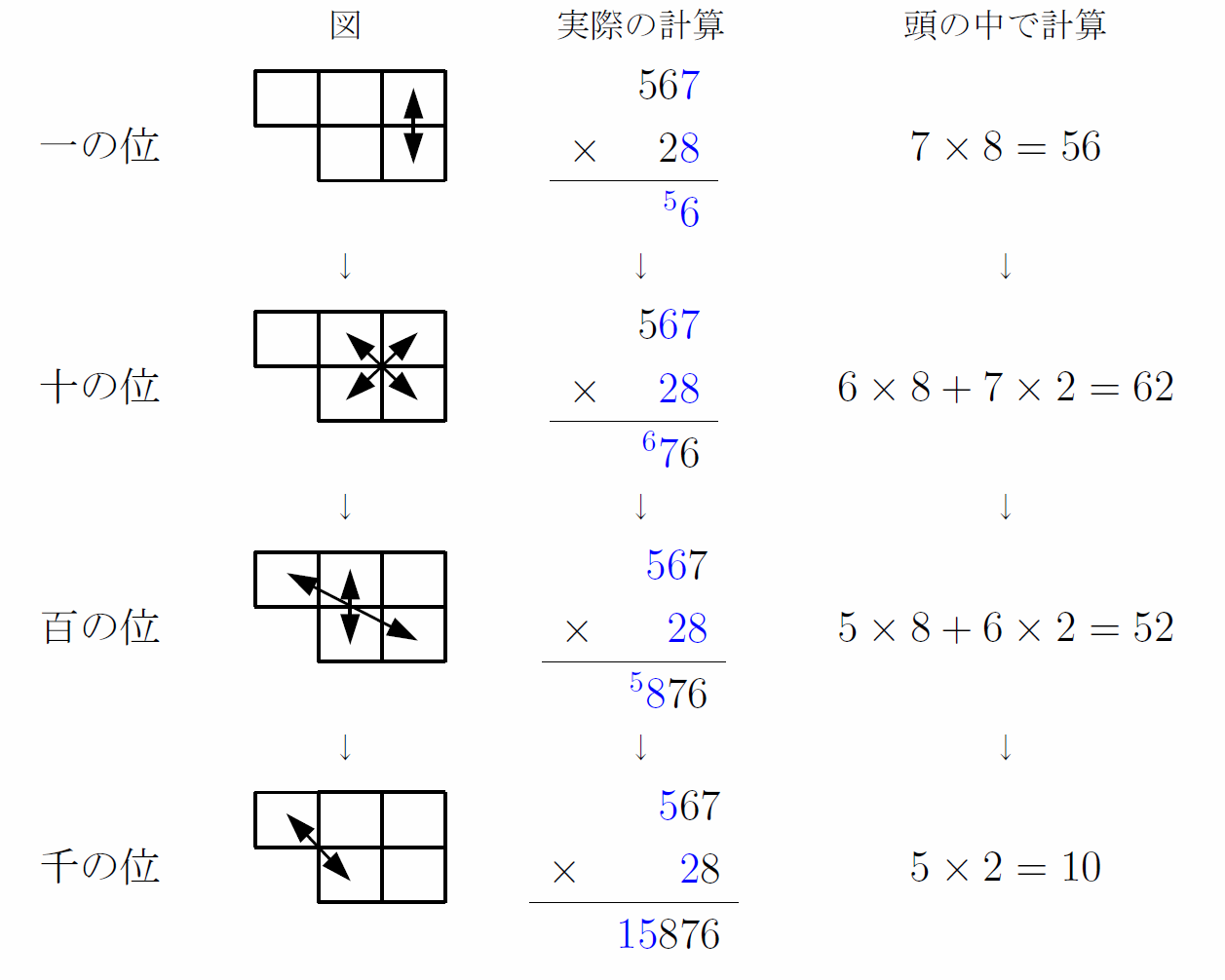
図でわかる3桁×2桁の万能速算術
3桁×2桁の場合は4段階に分けて桁ごとに計算できる。
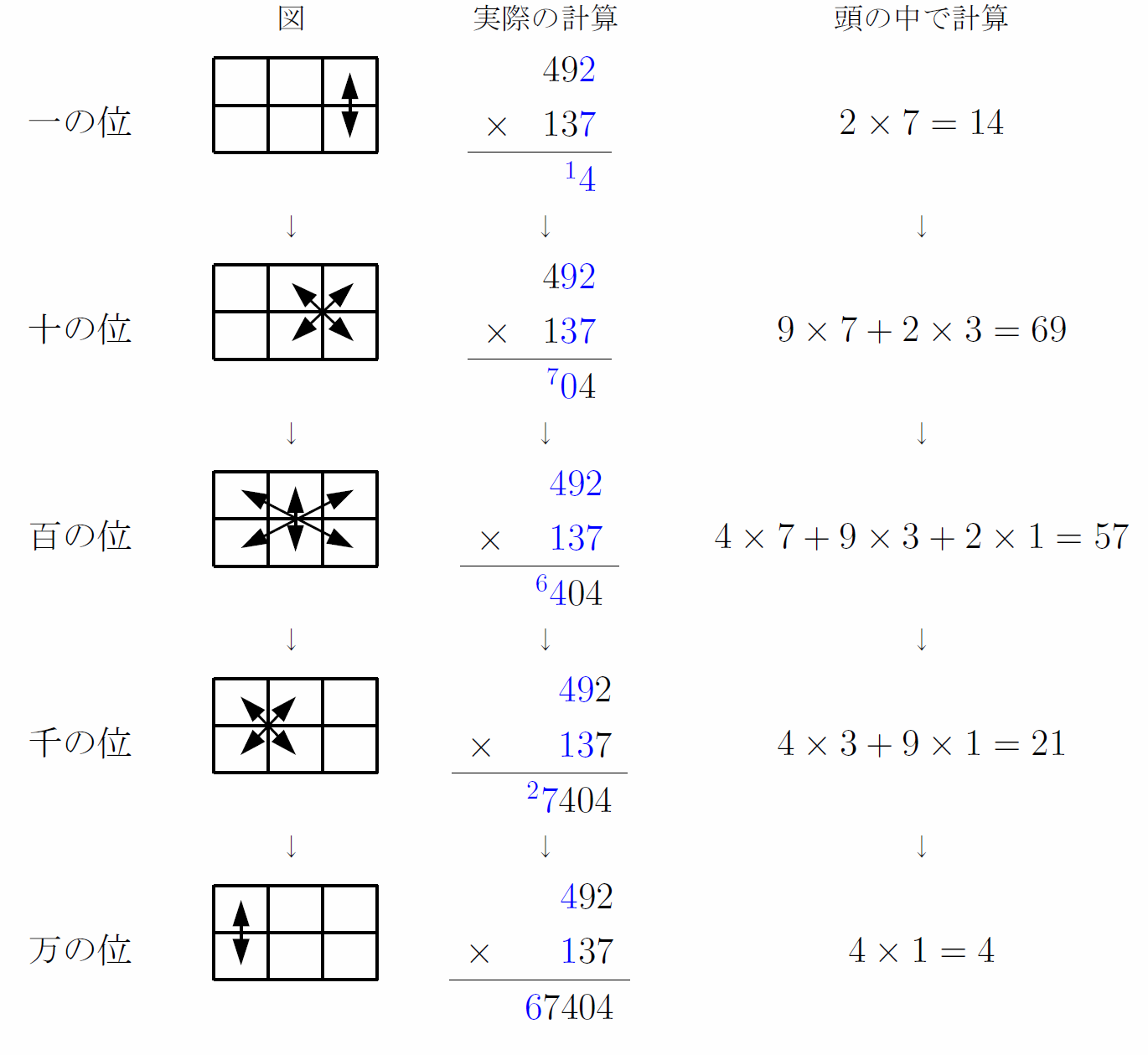
図でわかる3桁×3桁の万能速算術
3桁×3桁の場合は5段階に分けて桁ごとに計算できる.