音波 物質中を伝わる縦波(疎密波). 真空中では伝わらない(媒質が必要).
音源 振動して音を発生させる物体. 発音体ともいう.
空気中の音速 V
1気圧, 温度 t[℃] における音速
V = 331.5 + 0.6 t [m/s]
温度が高くなるほど音速が大きくなる.
音の三要素
大きさ 振動数 f が同じとき, 振幅 A が大きいほど音は大きい.
高さ 振動数 f が大きいほど高い音になる.
音色 波形の違いによって決まる.
可聴音 人が聴ける音の振動数の範囲. およそ 20 ~ 20000 Hz の範囲である.
超音波 可聴音の上限 20000 Hz を超える振動数の人が聴けない音.
音波の性質(様々な波に共通する現象)
反射
音波が物体に当たって跳ね返る現象.
例 山彦
例 魚群探知機・コウモリ: 音波を出し反射波を受け取るまでの時間で位置を把握.
回折
音波は波長が日常の物体並かそれ以上に長いため, 壁の背後にまで回り込んで届く.
干渉
2つの音源から同じ振動数の音を出すと, 音が強め合う場所と弱め合う場所ができる.
屈折
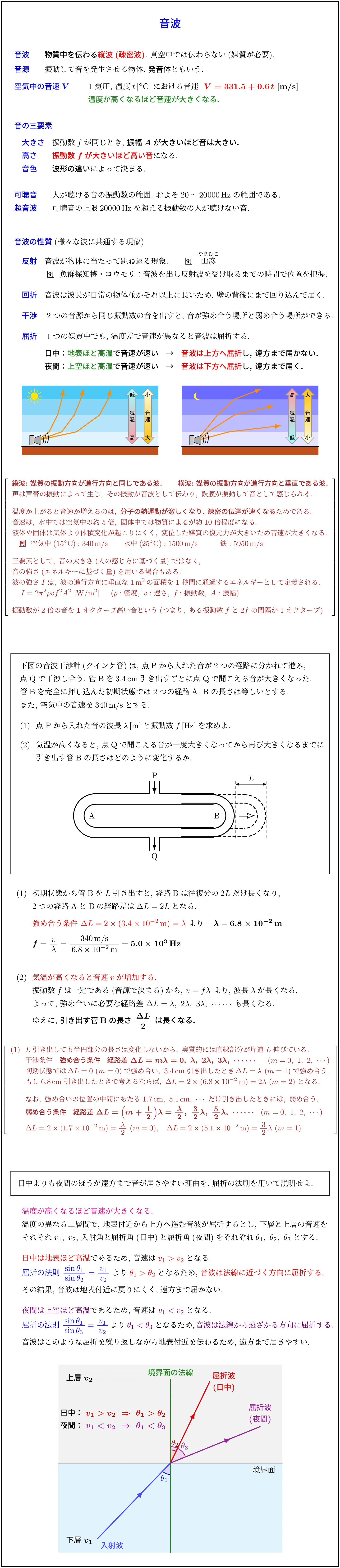
1つの媒質中でも, 温度差で音速が異なると音波は屈折する.
日中: 地表ほど高温で音速が速い → 音波は上方へ屈折し, 遠方まで届かない.
夜間: 上空ほど高温で音速が速い → 音波は下方へ屈折し, 遠方まで届く.
縦波: 媒質の振動方向が進行方向と同じである波.
横波: 媒質の振動方向が進行方向と垂直である波.
声は声帯の振動によって生じ, その振動が音波として伝わり, 鼓膜が振動して音として感じられる.
温度が上がると音速が増えるのは, 分子の熱運動が激しくなり, 疎密の伝達が速くなるためである.
音速は, 水中では空気中の約5倍, 固体中では物質によるが約10倍程度になる.
液体や固体は気体より体積変化が起こりにくく, 変位した媒質の復元力が大きいため音速が大きくなる.
例
空気中(15℃): 340 m/s
水中(25℃): 1500 m/s
鉄: 5950 m/s
三要素として, 音の大きさ(人の感じ方に基づく量)ではなく,
音の強さ(エネルギーに基づく量)を用いる場合もある.
波の強さ I は, 波の進行方向に垂直な 1 m² の面積を 1 秒間に通過するエネルギーとして定義される.
I = 2π² ρ v f² A² [W/m²]
(ρ: 密度, v: 速さ, f: 振動数, A: 振幅)
振動数が 2 倍の音を 1 オクターブ高い音という
(つまり, ある振動数 f と 2f の間隔が 1 オクターブ).
下図の音波干渉計(クインケ管)は, 点 P から入れた音が 2 つの経路に分かれて進み,
点 Q で干渉し合う.
管 B を 3.4 cm 引き出すごとに点 Q で聞こえる音が大きくなった.
管 B を完全に押し込んだ初期状態では 2 つの経路 A, B の長さは等しいとする.
また, 空気中の音速を 340 m/s とする.
(1) 点 P から入れた音の波長 λ[m] と振動数 f[Hz] を求めよ.
(2) 気温が高くなると, 点 Q で聞こえる音が一度大きくなってから再び大きくなるまでに
引き出す管 B の長さはどのように変化するか.
(1)
初期状態から管 B を L 引き出すと, 経路 B は往復分の 2L だけ長くなり,
2 つの経路 A と B の経路差は ΔL = 2L となる.
強め合う条件
ΔL = 2 × (3.4 × 10⁻² m) = λ
より
λ = 6.8 × 10⁻² m
f = v / λ = 340 m/s ÷ 6.8 × 10⁻² m = 5.0 × 10³ Hz
(2)
気温が高くなると音速 v が増加する.
振動数 f は一定である(音源で決まる)から, v = fλ より, 波長 λ が長くなる.
よって, 強め合いに必要な経路差
ΔL = λ, 2λ, 3λ, …
も長くなる.
ゆえに, 引き出す管 B の長さ ΔL / 2 は長くなる.
補足
L 引き出しても半円部分の長さは変化しないから, 実質的には直線部分が片道 L 伸びている.
干渉条件
強め合う条件 経路差
ΔL = mλ = 0, λ, 2λ, 3λ, … (m = 0,1,2,…)
初期状態では ΔL = 0 (m = 0) で強め合い,
3.4 cm 引き出したとき ΔL = λ (m = 1) で強め合う.
もし 6.8 cm 引き出したときで考えるならば,
ΔL = 2 × (6.8 × 10⁻² m) = 2λ (m = 2) となる.
なお, 強め合いの位置の中間にあたる
1.7 cm, 5.1 cm, … だけ引き出したときには, 弱め合う.
弱め合う条件 経路差
ΔL = (m + 1/2) λ = λ/2, 3/2 λ, 5/2 λ, … (m = 0,1,2,…)
ΔL = 2 × (1.7 × 10⁻² m) = λ/2 (m = 0)
ΔL = 2 × (5.1 × 10⁻² m) = 3/2 λ (m = 1)
日中よりも夜間のほうが遠方まで音が届きやすい理由を, 屈折の法則を用いて説明せよ.
温度が高くなるほど音速が大きくなる.
温度の異なる二層間で, 地表付近から上方へ進む音波が屈折するとし,
下層と上層の音速をそれぞれ v₁, v₂,
入射角と屈折角(日中)と屈折角(夜間)をそれぞれ θ₁, θ₂, θ₃ とする.
日中は地表ほど高温であるため, 音速は v₁ > v₂ となる.
屈折の法則
sinθ₁ / sinθ₂ = v₁ / v₂
より θ₁ > θ₂ となるため, 音波は法線に近づく方向に屈折する.
その結果, 音波は地表付近に戻りにくく, 遠方まで届かない.
夜間は上空ほど高温であるため, 音速は v₁ < v₂ となる.
屈折の法則
sinθ₁ / sinθ₃ = v₁ / v₂
より θ₁ < θ₃ となるため, 音波は法線から遠ざかる方向に屈折する.
音波はこのような屈折を繰り返しながら次第に地表側へ曲がり, 地表付近を伝わるため, 遠方まで届きやすい.

