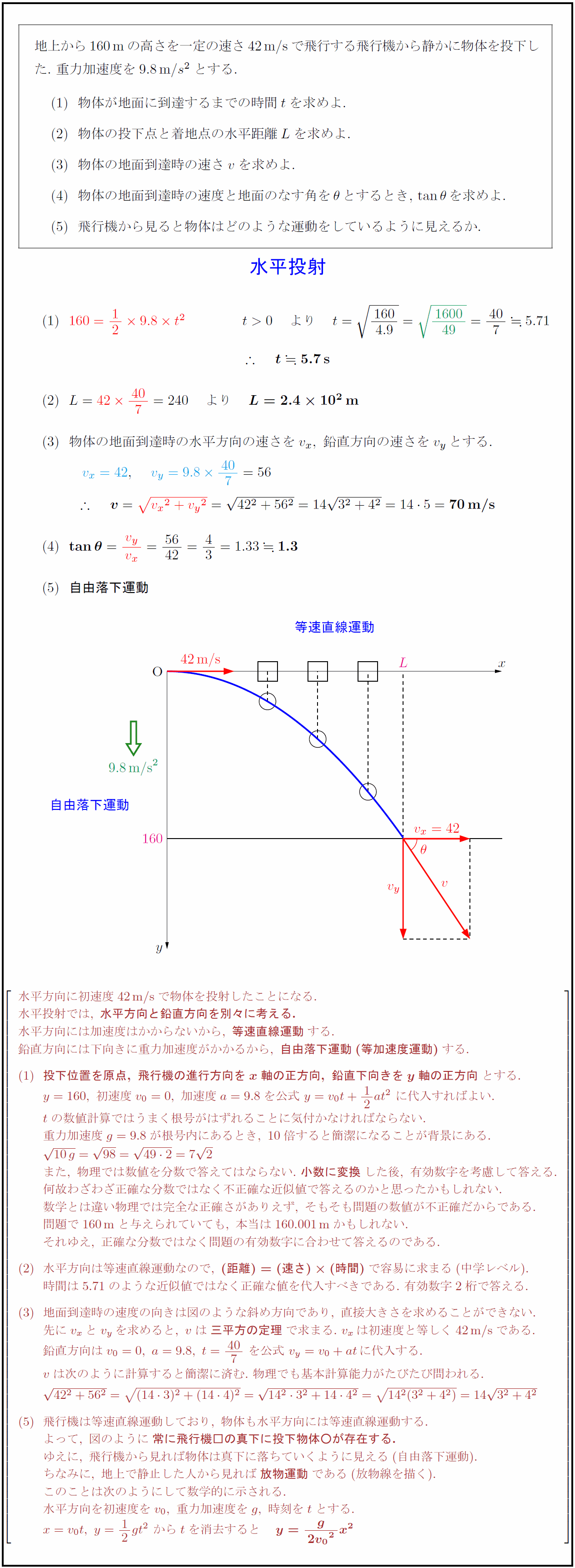
地上から160mの高さを一定の速さ42m/sで飛行する飛行機から静かに物体を投下し た.\ 重力加速度を$9.8$m/$s²$とする. 物体が地面に到達するまでの時間$t$を求めよ. 物体の投下点と着地点の水平距離$L$を求めよ. 物体の地面到達時の速さ$v$を求めよ. 物体の地面到達時の速度と地面のなす角を$θ$とするとき,\ $tanθ$を求めよ. 飛行機から見ると物体はどのような運動をしているように見えるか. $物体の地面到達時の水平方向の速さをv_x,\ 鉛直方向の速さをv_yとする.$ 等速直線運動} {(-1,-4)}[w]{自由落下運動} 水平方向に初速度42m/s}で物体を投射したことになる. 水平投射では,\ {水平方向と鉛直方向を別々に考える.} 水平方向には加速度はかからないから,\ {等速直線運動}する. 鉛直方向には下向きに重力加速度がかかるから,\ {自由落下運動(等加速度運動)}する. {投下位置を原点,\ 飛行機の進行方向をx軸の正方向,\ 鉛直下向きをy軸の正方向}とする. y=160,\ 初速度v₀=0,\ 加速度a=9.8を公式\ y=v₀t+12at²\ に代入すればよい. tの数値計算ではうまく根号がはずれることに気付かなければならない. 重力加速度g=9.8が根号内にあるとき,\ 10倍すると簡潔になることが背景にある. {10g}={98}={492}=72\ また,\ 物理では数値を分数で答えてはならない.\ {小数に変換}した後,\ 有効数字を考慮して答える. 何故わざわざ正確な分数ではなく不正確な近似値で答えるのかと思ったかもしれない. 数学とは違い物理では完全な正確さがありえず,\ そもそも問題の数値が不正確だからである. 問題で160m}と与えられていても,\ 本当は160.001m}かもしれない. それゆえ,\ 正確な分数ではなく問題の有効数字に合わせて答えるのである. 水平方向は等速直線運動なので,\ {(距離)=(速さ)(時間)}で容易に求まる(中学レベル). 時間は5.71のような近似値ではなく正確な値を代入すべきである.\ 有効数字2桁で答える. 地面到達時の速度の向きは図のような斜め方向であり,\ 直接大きさを求めることができない. 先にv_xとv_yを求めると,\ vは{三平方の定理}で求まる.\ v_xは初速度と等しく42m/s}である. 鉛直方向はv₀=0,\ a=9.8,\ t={40}{7}\ を公式\ v_y=v₀+atに代入する. vは次のように計算すると簡潔に済む.\ 物理でも基本計算能力がたびたび問われる. {42²+56²}={(143)²+(144)²}={14²3²+144²}={14²(3²+4²)}=14{3²+4²} 飛行機は等速直線運動しており,\ 物体も水平方向には等速直線運動する. よって,\ 図のように{常に飛行機□の真下に投下物体○が存在する.} ゆえに,\ 飛行機から見れば物体は真下に落ちていくように見える(自由落下運動). ちなみに,\ 地上で静止した人から見れば{放物運動}である(放物線を描く). このことは次のようにして数学的に示される. 水平方向を初速度をv₀,\ 重力加速度をg,\ 時刻をtとする. x=v₀t,\ y=12gt²\ からtを消去すると {y={g}{2{v₀}²}x²}

