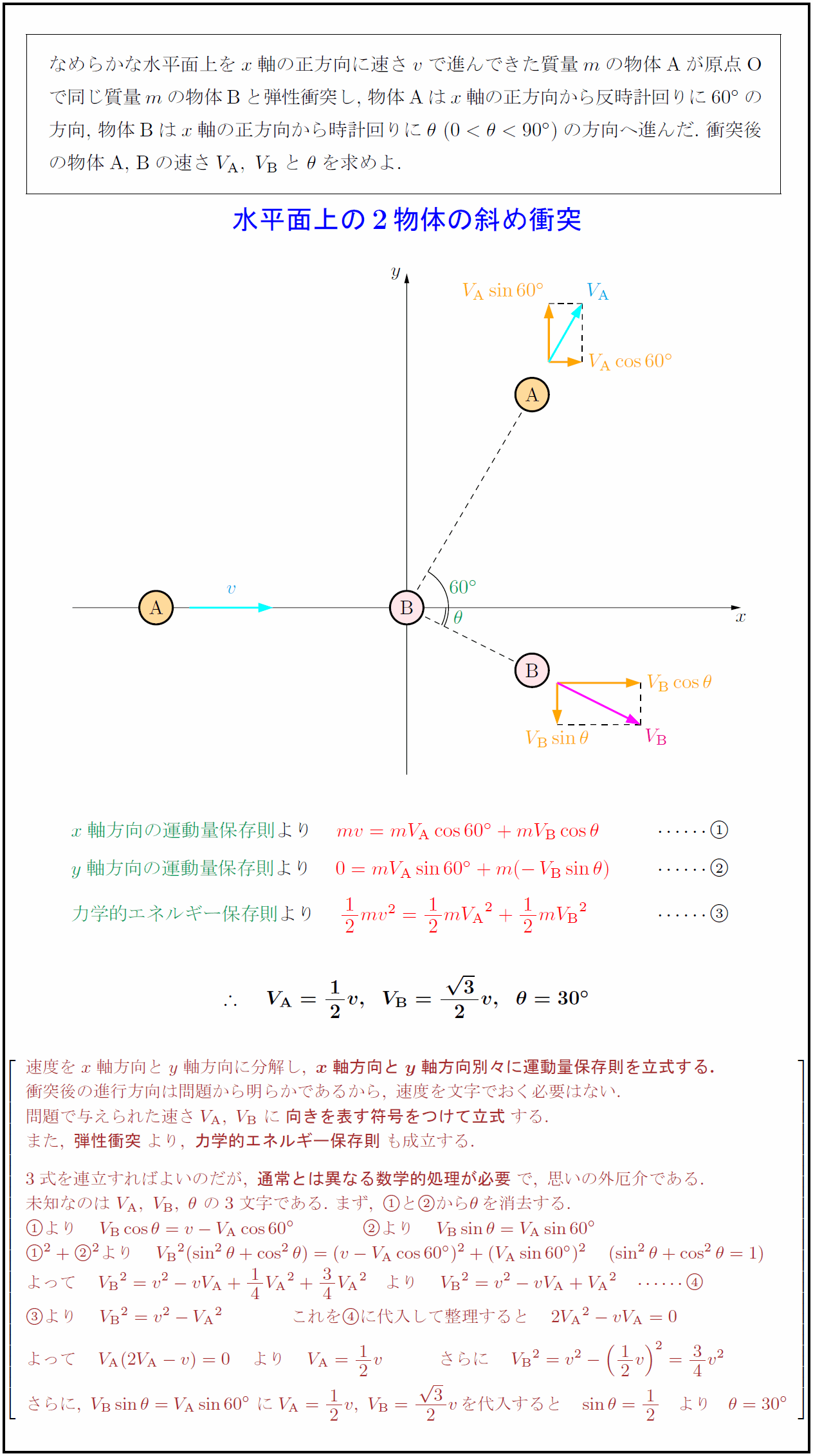
なめらかな水平面上を$x$軸の正方向に速さ$v$で進んできた質量$m$の物体Aが原点O で同じ質量$m$の物体Bと弾性衝突し,\ 物体Aは$x$軸の正方向から反時計回りに$60°$の 方向,\ 物体Bは$x$軸の正方向から反時計回りに$θ\ (0<θ<90°)$の方向へ進んだ.\ 衝突 後の物体A,\ Bの速さ$V_{ A},\ V_{ B}$と$θ$を求めよ. 水平面上の2物体の斜め衝突 $x$軸方向の運動量保存則}より $mv=mV_{ A}cos60°+mV_{ B}cosθ}$ & $$ $y$軸方向の運動量保存則}より $0=mV_{ A}sin60°+m(-V_{ B}sinθ)}$ & $$ 力学的エネルギー保存則}より 速度をx軸方向とy軸方向に分解し,\ {x軸方向とy軸方向別々に運動量保存則を立式する.} 衝突後の進行方向は問題から明らかであるから,\ 速度を文字でおく必要はない. 問題で与えられた速さV_{ A},\ V_{ B}\ に{向きを表す符号をつけて立式}する. また,\ {弾性衝突}より,\ {力学的エネルギー保存則}も成立する. 3式を連立すればよいのだが,\ {通常とは異なる数学的処理が必要}で,\ 思いの外厄介である. 未知なのは\ V_{ A},\ V_{ B},\ θ\ の3文字である.\ まず,\ とからθを消去する.

