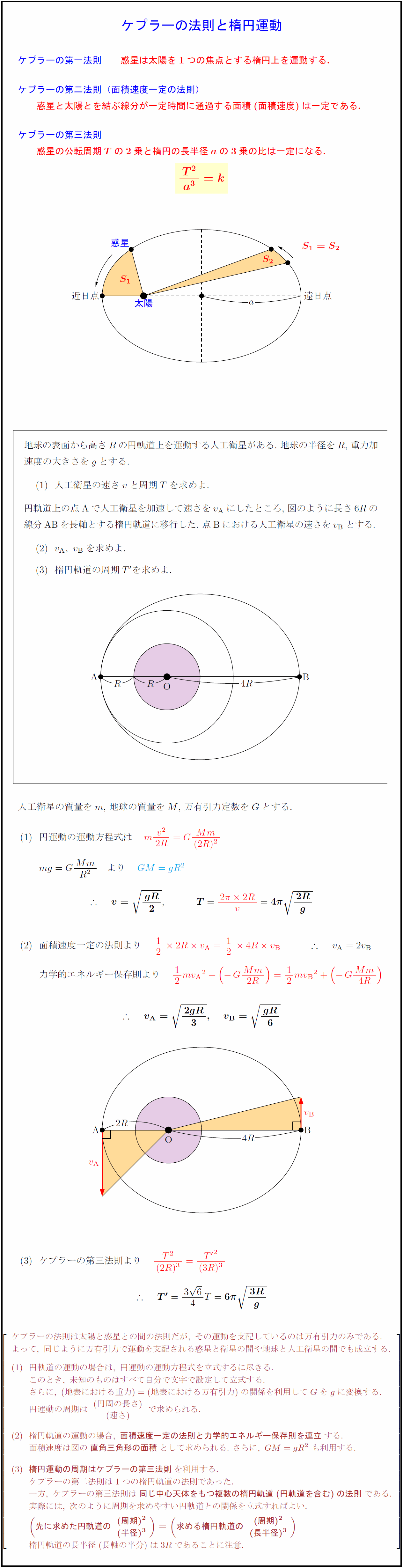
ケプラーの第一法則 惑星は太陽を1つの焦点とする楕円上を運動する. ケプラーの第二法則(面積速度一定の法則) 惑星と太陽とを結ぶ線分が一定時間に通過する面積(面積速度)は一定である. ケプラーの第三法則 惑星の公転周期${T}$の2乗と楕円の長半径${a}$の3乗の比は一定になる. \E[s]{太陽} \F[nw]{惑星} \A[e]{遠日点} \C[w]{近日点} 地球の表面から高さ$R$の円軌道上を運動する人工衛星がある.\ 地球の半径を$R$,\ 重力加 速度の大きさを$g$とする.\ 人工衛星の速さ$v$と周期$T$を求めよ. 円軌道上の点Aで人工衛星を加速して速さを$v_{ A}$にしたところ,\ 図のように長さ$6R$の .97}{線分ABを長軸とする楕円軌道に移行した.\ 点Bにおける人工衛星の速さを$v_{ B}$とする.} $v_{ A},\ v_{ B}$を求めよ. $楕円軌道の周期T’を求めよ 人工衛星の質量を$m$,\ 地球の質量を$M$,\ 万有引力定数を$G$とする. 円運動の運動方程式は { }力学的エネルギー保存則より ケプラーの法則は太陽と惑星との間の法則だが,\ その運動を支配しているのは万有引力のみである. よって,\ 同じように万有引力で運動を支配される惑星と衛星の間や地球と人工衛星の間でも成立する. 円軌道の運動の場合は,\ 円運動の運動方程式を立式するに尽きる. このとき,\ 未知のものはすべて自分で文字で設定して立式する. さらに,\ (地表における重力)=(地表における万有引力)の関係を利用してGをgに変換する. 円運動の周期は\ {(円周の長さ)}{(速さ)}\ で求められる. 楕円軌道の運動の場合,\ {面積速度一定の法則と力学的エネルギー保存則を連立}する. 面積速度は図の{直角三角形の面積}として求められる.\ さらに,\ GM=gR²\ も利用する. {楕円運動の周期はケプラーの第三法則}を利用する. ケプラーの第二法則は1つの楕円軌道の法則であった. 一方,\ ケプラーの第三法則は{同じ中心天体をもつ複数の楕円軌道(円軌道を含む)の法則}である. 実際には,\ 次のように周期を求めやすい円軌道との関係を立式すればよい. {(先に求めた円軌道の\ {(周期)²}{(半径)³})=(求める楕円軌道の\ {(周期)²}{(長半径)³})} 楕円軌道の長半径(長軸の半分)は3Rであることに注意.

