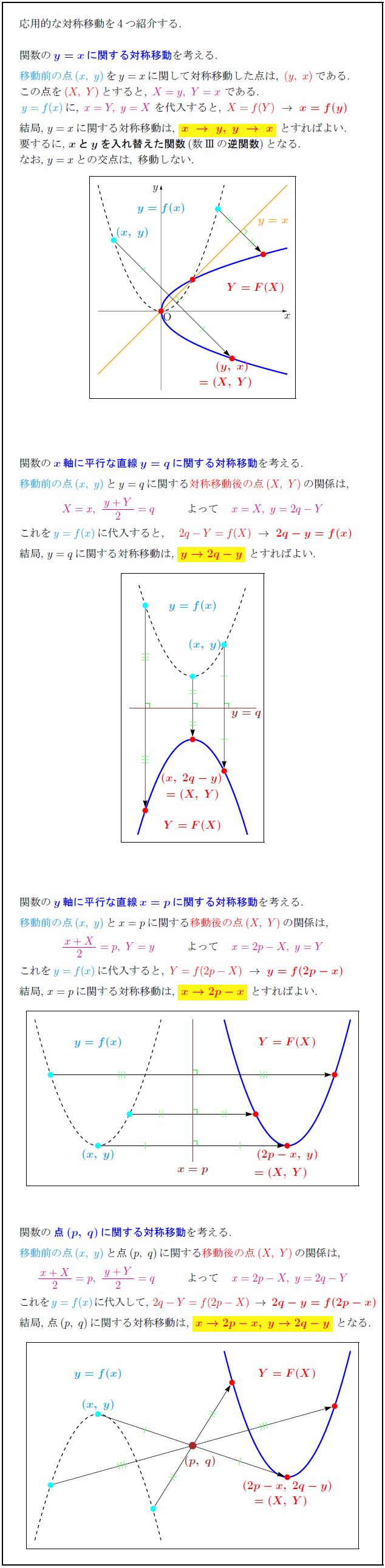
応用的な対称移動を4つ紹介する. 関数の${y=xに関する対称移動を考える.$ 移動前の点}$(x,\ y)}をy=xに関して対称移動した点は,\ (y,\ x)}である.$ この点を$(X,\ Y)}とすると,\ X=y,\ Y=x}\ である.$ $y=f(x)}に,\ x=Y,\ y=X}\ を代入すると,\ X=f(Y)}\ →\ {x=f(y)$ 結局,\ $y=x$に関する対称移動は,\ yellow}{${x\ →\ y,\ y\ →\ x$}\ とすればよい. 要するに,\ ${xとy}$を入れ替えた関数}(数IIIの逆関数})となる. なお,\ $y=xとの交点は,\ 移動しない.$ 関数の${x軸に平行な直線y=qに関する対称移動を考える.$ 移動前の点}$(x,\ y)}とy=qに関する対称移動後の点(X,\ Y)}の関係は,$ $X=x,\ {y+Y}{2}=q} よって x=X,\ y=2q-Y}$} これを$y=f(x)}に代入すると, 2q-Y=f(X)}\ →\ {2q-y=f(x)$ 結局,\ $y=q$に関する対称移動は,\ yellow}{${y→2q-y 関数の${y軸に平行な直線x=pに関する対称移動を考える.$ 移動前の点}$(x,\ y)}とx=pに関する移動後の点(X,\ Y)}の関係は,$ ${x+X}{2}=p,\ Y=y} よって x=2p-X,\ y=Y}$} これを$y=f(x)}に代入すると,\ Y=f(2p-X)}\ →\ {y=f(2p-x)$ 結局,\ $x=p$に関する対称移動は,\ yellow}{${x→2p-x$}\ とすればよい. 関数の${点(p,\ q)に関する対称移動を考える.$ 移動前の点}$(x,\ y)}と点(p,\ q)に関する移動後の点(X,\ Y)}の関係は,$ ${x+X}{2}=p,\ {y+Y}{2}=q} よって x=2p-X,\ y=2q-Y}$} これを$y=f(x)}に代入して,\ 2q-Y=f(2p-X)}\ →\ {2q-y=f(2p-x)$ 結局,\ $点(p,\ q)$に関する対称移動は,\ yellow}{${x→2p-x,\ y→2q-y$}\ となる.

