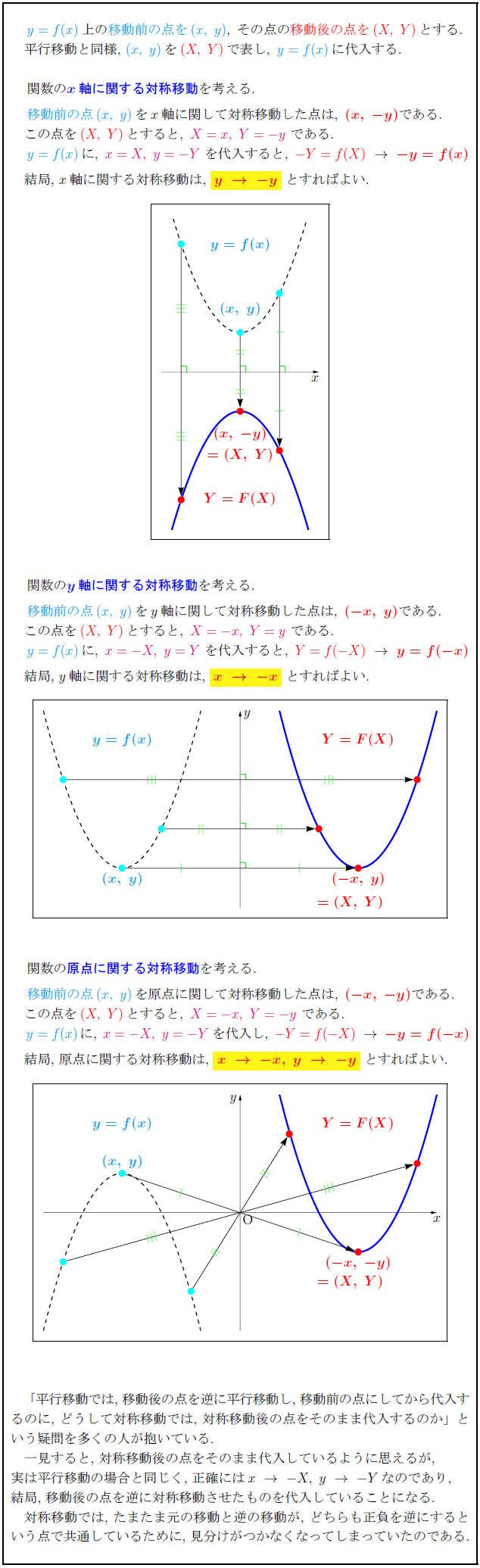
$y=f(x)}上の移動前の点を(x,\ y)},\ その点の移動後の点を(X,\ Y)}とする.$ 平行移動と同様,\ $(x,\ y)}を(X,\ Y)}で表し,\ y=f(x)}に代入する.$ $関数の{x軸に関する対称移動を考える.$ $移動前の点(x,\ y)}をx軸に関して対称移動した点は,\ 結局,\ $x$軸に関する対称移動は,\ $関数の{y軸に関する対称移動を考える.$ $移動前の点(x,\ y)}をy軸に関して対称移動した点は,\ $関数の原点に関する対称移動を考える.$ $移動前の点(x,\ y)}を原点に関して対称移動した点は,\ \ 結局,\ 原点に関する対称移動は 「平行移動では,\ 移動後の点を逆に平行移動し,\ 移動前の点にしてから代入するのに,\ どうして対称移動では,\ 対称移動後の点をそのまま代入するのか」という疑問を多くの人が抱いている. 一見すると,\ 対称移動後の点をそのまま代入しているように思えるが, 実は平行移動の場合と同じく,\ 正確には$x\ →\ -X,\ y\ →\ -Y$なのであり, 結局,\ 移動後の点を逆に対称移動させたものを代入していることになる. 対称移動では,\ たまたま元の移動と逆の移動が,\ どちらも正負を逆にするという点で共通しているために,\ 見分けがつかなくなってしまっていたのである.

