定期試験レベルの基本問題です。
問題
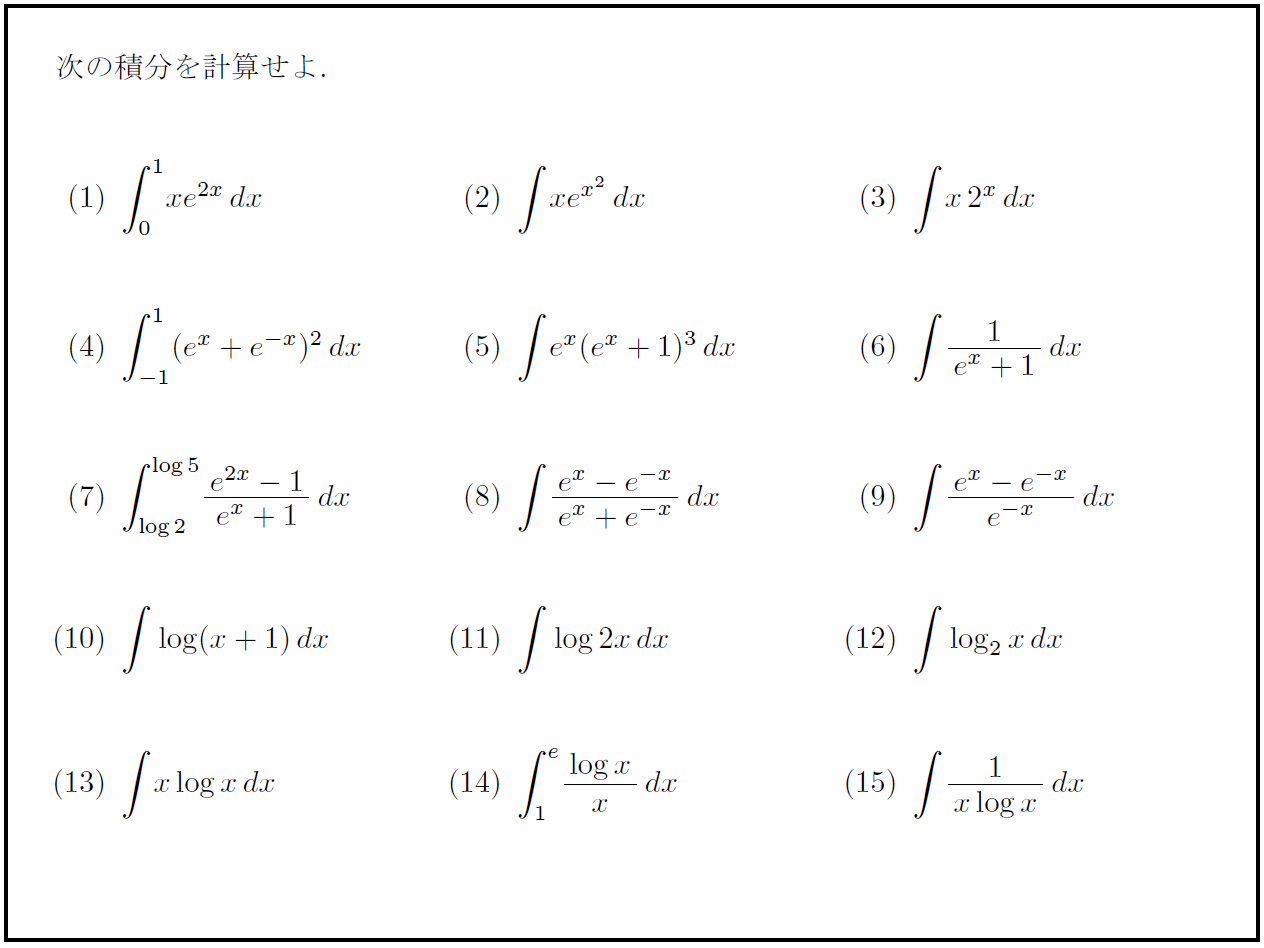
解答

x^me^{nx}型はe^{nx}を微分形とみて部分積分する.$ $部分積分の公式 $(x²)’=2xが接触しているので,\ 微分形接触型である.$ $x^ma^{nx}型はa^{nx}を微分形とみて部分積分する.\ ∫a^xdx={a^x}{log a}+C\ は忘れやすいので注意.$ 積分区間が対称なので,\ まず偶関数・奇関数の可能性を探る. $f(x)=e^x+e^{-x}\ とすると\ f(-x)=e^{-x}+e^x=f(x)\ より,\ f(x)は偶関数である.$ $e^x$だけでは偶関数でも奇関数でもないが,\ 全体でみると対称性をもつことがある. 微分形接触累乗型であるから瞬殺できる. 微分形接触型であるから,\ 当然置換積分で求めることもできる(別解). 最悪,\ 展開してから普通に積分することもできる. $分子に分母と同じ形を作ってからつじつまを合わせると,\ 分子が分母の微分型に帰着する.$ $常にe^x>0より,\ 絶対値ははずすことができる.$ $e^xのみからなる関数は,\ 最悪e^x=tとおけばtのみの積分に帰着する.$ 本問の場合,\ 置換後に部分分数分解が必要になる. ${1}{(t+1)t}={A}{t+1}+{B}{t}\ とおいて分母をはらうと 1=At+B(t+1)$ $t=-1としてA=-1,t=0としてB=1を得る.$ $e^x=tとおいても積分できるが,\ 分子を因数分解すると約分できることに気付くべきである.$ $対数の定義\ a^p=Mp=log_aM\ より,\ 一般に\ a^{log_aM}=M\ が成り立つ.$ $よって,\ e^{log5}=5,\ e^{log2}=2\ である.$\ 最後,\ $3-log₅2$と答えてもよい. $e^x=t\ とおいても積分できるが,\ 分子が分母の微分型であることに気付くべきである.$ 分数の積分では,\ この型の確認が何よりも優先すべきであることを忘れてはならない. 常に$e^x>0,\ e^{-x}>0$であるから,\ 絶対値ははずせる. 分母が1つの項なので,\ 分割してから積分すればよいだけである. $log 単独の積分は,\ (x)’log xとみなして部分積分するのが基本である.$ $ただし,\ 本問の場合は後の約分を見越して(x)’ではなく(x+1)’とみると楽になる(本解).$ $(x)’とみなした場合は分子の次数下げが必要になる. {x}{x+1}={(x+1)-1}{x+1}=1-{1}{x+1}$ $また,\ 問題がlog(x+1)なのでx+1>0が確定しており,\ 絶対値をつける必要はない.$ $公式\ ∫log xdx=xlog x-x+C$の1次式置換型と考えると瞬殺できる(別解2). 公式\ $∫log xdx=xlog x-x+Cの1次式置換型と考えると瞬殺できる.$ 対数の性質\ $log MN=log M+log N$\ を利用することもできる(別解). 底の変換公式\ $log_ab={log_cb}{log_ca}$\ で底を自然対数にした後,\ 公式を適用する. $x^m(log x)^n型は,\ x^mを微分形と見て部分積分する.$ $x^m(log x)^n型であるが,\ 特にn=-1の場合のみ微分形接触型の扱いになる.$ つまり,\ $(log x)’=1x\ が接触しているから,\ log x=tと置換する.$ 定積分において置換した場合,\ 積分区間が変わることを忘れないように注意する. 微分形接触累乗型\ $∫{f(x)}^{α}f'(x)dx=f(x)}^{α+1{α+1}+C$\ とみなせれば瞬殺できる(別解). 前問と同じ微分形接触型なので,\ $log x=t$\ とおいて求めることも当然できる. しかし,\ 分子が分母の微分型とみなして瞬殺すべきである. この型は微分形が分数になると見抜きにくくなるので,\ 演習が必要である.

