以下の楕円バージョンです。
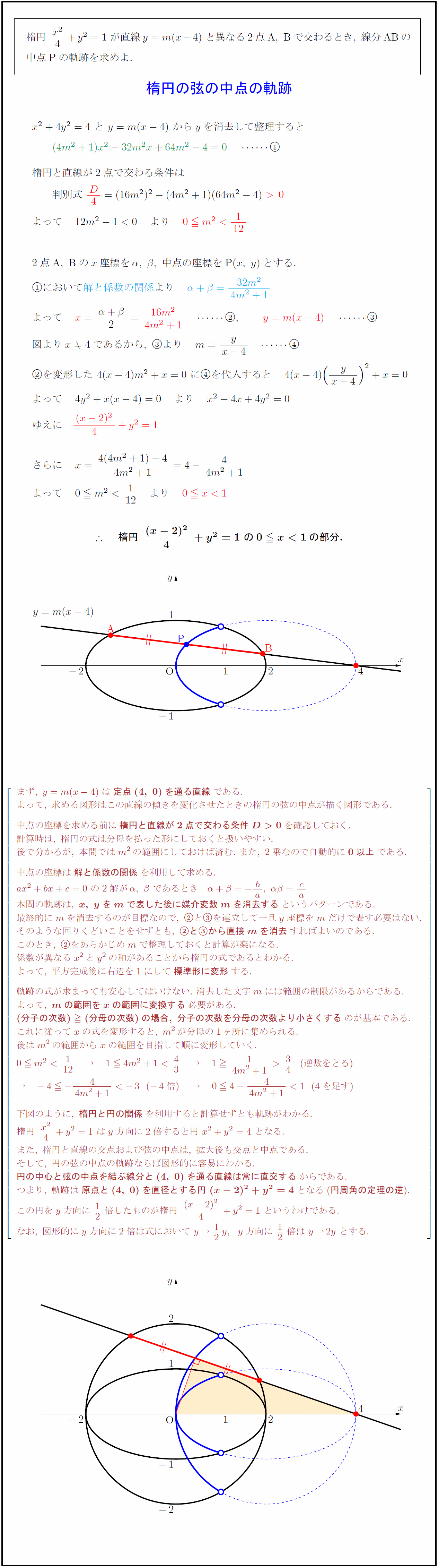
楕円\ {x²}{4}+y²=1\ が直線y=m(x-4)\ と異なる2点{A,\ B}で交わるとき,\ 線分{AB}の$ $中点{P}の軌跡を求めよ.$ $x²+4y²=4\ と\ y=m(x-4)\ からyを消去して整理すると$ $(4m²+1)x²-32m²x+64m²-4=0} $ $楕円と直線が2点で交わる条件は$ $判別式\ D4}=(16m²)²-(4m²+1)(64m²-4)\ 0}$ $よって 12m²-10 より 0 m²{1}{12$ $2点{A,\ B}のx座標をα,\ β,\ 中点の座標を{P}(x,\ y)とする.$ $において解と係数の関係}より まず,\ y=m(x-4)は{定点(4,\ 0)を通る直線}である. よって,\ 求める図形はこの直線の傾きを変化させたときの楕円の弦の中点が描く図形である. 中点の座標を求める前に{楕円と直線が2点で交わる条件D0}を確認しておく. 計算時は,\ 楕円の式は分母を払った形にしておくと扱いやすい. 後で分かるが,\ 本問ではm²の範囲にしておけば済む.\ また,\ 2乗なので自動的に{0以上}である. 中点の座標は{解と係数の関係}を利用して求める. ax²+bx+c=0\ の2解がα,\ β\ であるとき α+β=- ba,\ αβ= ca 本問の軌跡は,\ {x,\ yをmで表した後に媒介変数mを消去する}というパターンである. 最終的にmを消去するのが目標なので,\ とを連立して一旦y座標をmだけで表す必要はない. そのような回りくどいことをせずとも,\ {とから直接mを消去}すればよいのである. このとき,\ をあらかじめmで整理しておくと計算が楽になる. 係数が異なるx²とy²の和があることから楕円の式であるとわかる. よって,\ 平方完成後に右辺を1にして{標準形に変形}する. 軌跡の式が求まっても安心してはいけない.\ 消去した文字mには範囲の制限があるからである. よって,\ {mの範囲をxの範囲に変換する}必要がある. {(分子の次数)(分母の次数)の場合,\ 分子の次数を分母の次数より小さくする}のが基本である. これに従ってxの式を変形すると,\ m²が分母の1ヶ所に集められる. 後はm²の範囲からxの範囲を目指して順に変形していく. 0 m²{1}{12} → 14m²+143 → 1{1}{4m²+1}34(逆数をとる) → -4-{4}{4m²+1}-3(-4倍) → 04-{4}{4m²+1}1(4を足す) 下図のように,\ {楕円と円の関係}を利用すると計算せずとも軌跡がわかる. 楕円\ {x²}{4}+y²=1\ はy方向に2倍すると円\ x²+y²=4\ となる. また,\ 楕円と直線の交点および弦の中点は,\ 拡大後も交点と中点である. そして,\ 円の弦の中点の軌跡ならば図形的に容易にわかる. {円の中心と弦の中点を結ぶ線分と(4,\ 0)を通る直線は常に直交する}からである. つまり,\ 軌跡は{原点と(4,\ 0)を直径とする円\ (x-2)²+y²=4}となる({円周角の定理の逆}). この円をy方向に12倍したものが楕円\ {(x-2)²}{4}+y²=1\ というわけである. なお,\ 図形的にy方向に2倍は式において\ y→12y,y方向に12倍は\ y→2y\ とする.


