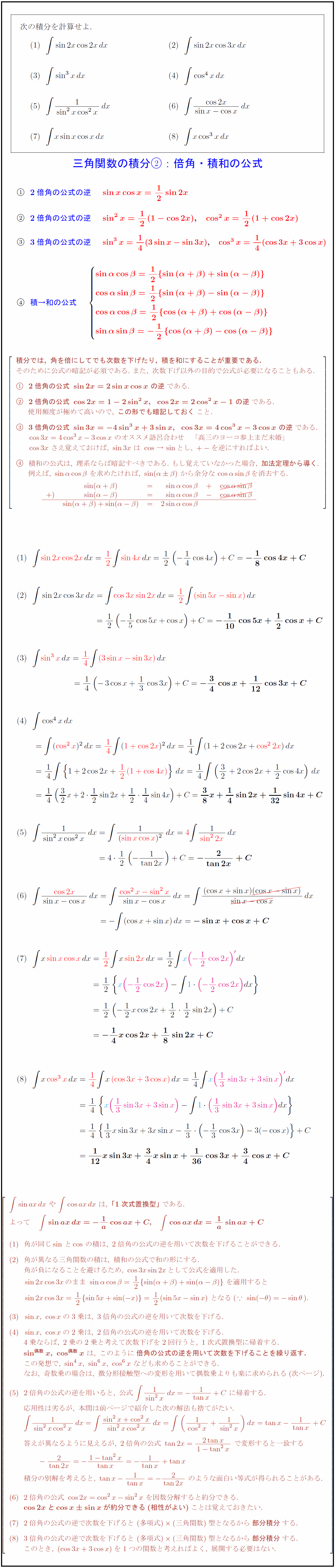
∫sin2xcos2xdx ∫sin2xcos3xdx ∫sin³xdx ∫cos⁴xdx ∫1/(sin²xcos²x)dx ∫cos2x/(sinx-cosx)dx ∫xsinxcosxdx ∫xcos³xdx 次の積分を計算せよ. 三角関数の積分:倍角・積和の公式{2倍角の公式の逆{3倍角の公式の逆{積→和の公式 {積分では,\ 角を倍にしてでも次数を下げたり,\ 積を和にすることが重要である.} そのために公式の暗記が必須である.\ また,\ 次数下げ以外の目的で公式が必要になることもある. {2倍角の公式\ sin 2x=2sin xcos x\ の逆}である. {2倍角の公式\ cos2x=1-2sin²x,cos2x=2cos²x-1\ の逆}である. 使用頻度が極めて高いので,\ {この形でも暗記しておく}こと. {3倍角の公式\ sin3x=-4sin³x+3sin x,cos3x=4cos³x-3cos x\ の逆}である. cos3x=4cos³x-3cos x\ のオススメ語呂合わせ 「高三のヨーコ参上まだ未婚」 cos3x\ さえ覚えておけば,\ sin 3x\ は\ cos→sin とし,\ +-を逆にすればよい. 積和の公式は,\ 理系ならば暗記すべきである.\ もし覚えていなかった場合,\ {加法定理から導く}. 例えば,\ sinαcosβ\ を求めたければ,\ sin(αβ)\ から余分なcosαsinβを消去する. 「1次式置換型」}である. 角が同じsinとcosの積は,\ 2倍角の公式の逆を用いて次数を下げることができる. 角が異なる三角関数の積は,\ 積和の公式で和の形にする. 角が負になることを避けるため,\ cos3xsin2xとして公式を適用した. sin x,\ cos xの3乗は,\ 3倍角の公式の逆を用いて次数を下げる. sin x,\ cos xの2乗は,\ 2倍角の公式の逆を用いて次数を下げる. 4乗ならば,\ 2乗の2乗と考えて次数下げを2回行うと,\ 1次式置換型に帰着する. {sin^{偶数}x,\ cos^{偶数}x}\ は,\ このように{倍角の公式の逆を用いて次数を下げることを繰り返す.} この発想で,\ sin⁴x,\ sin^6x,\ cos^6x\ なども求めることができる. なお,\ 奇数乗の場合は,\ 微分形接触型への変形を用いて偶数乗よりも楽に求められる(次ページ). 2倍角の公式の逆を用いると,\ 公式\ ∫{1}{sin²x}dx=-{1}{tan x}+C\ に帰着する. 応用性は劣るが,\ 本問は,\ 前ページで紹介した次の解法も捨てがたい. 答えが異なるように見えるが,\ 2倍角の公式\ tan2x={2tan x}{1-tan²x}\ で変形すると一致する 積分の別解を考えると,\ tan x-{1}{tan x}=-{2}{tan2x}\ のような面白い等式が得られることがある. 2倍角の公式\ cos2x=cos²x-sin²x\ を因数分解すると約分できる. {cos2xとcos xsin xが約分できる(相性がよい)}ことは覚えておきたい. 2倍角の公式の逆で次数を下げると\ (多項式)(三角関数)型となるから{部分積分}する. 3倍角の公式の逆で次数を下げると\ (多項式)(三角関数)型となるから{部分積分}する. このとき,\ (cos3x+3cos x)を1つの関数と考えればよく,\ 展開する必要はない.

