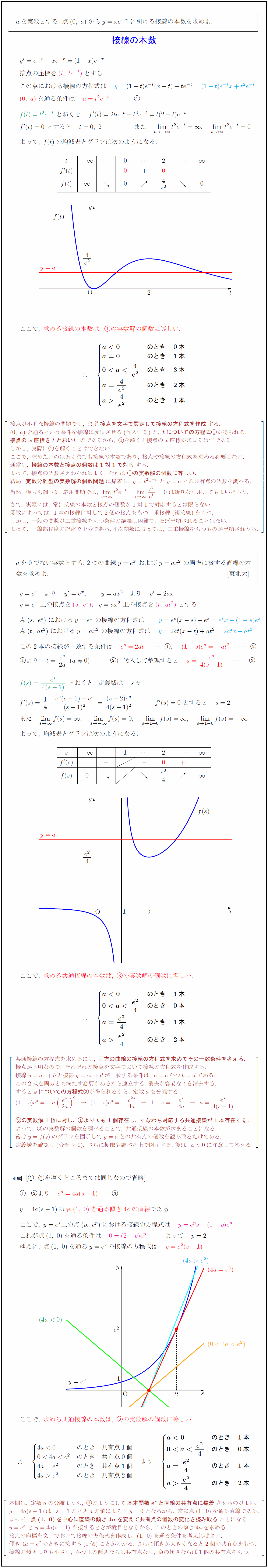
aを実数とする.\ 点(0,\ a)からy=xe^{-x}\ に引ける接線の本数を求めよ.$ $接点の座標を $よって,\ f(t)の増減表とグラフは次のようになる.$ 接点が不明な接線の問題では,\ まず{接点を文字で設定して接線の方程式を作成}する. (0,\ a)を通るという条件を接線に反映させる(代入する)と,\ {tについての方程式}が得られる. {接点のx座標をtとおいた}のであるから,\ を解くと接点のx座標が求まるはずである. しかし,\ 実際にを解くことはできない. ここで,\ 求めたいのはあくまでも接線の本数であり,\ 接点や接線の方程式を求める必要はない. 通常は,\ {接線の本数と接点の個数は1対1で対応}する. よって,\ 接点の個数さえわかればよく,\ それは{の実数解の個数に等しい.} 結局,\ {定数分離型の実数解の個数問題}に帰着し,\ y=t²e^{-t}\ と\ y=aとの共有点の個数を調べる. 当然,\ 極限も調べる.\ 応用問題では,\ limt→∞}t²e^{-t}=limt→∞}{t²}{e^t}=0\ は断りなく用いてもよいだろう. さて,\ 実際には,\ 常に接線の本数と接点の個数が1対1で対応するとは限らない. 関数によっては,\ 1本の接線に対して2個の接点をもつ二重接線(複接線)をもつ. しかし,\ 一般の関数が二重接線をもつ条件の議論は困難で,\ ほぼ出題されることはない. よって,\ 下線部程度の記述で十分である.\ 4次関数に限っては,\ 二重接線をもつものが出題されうる. aを0でない実数とする.\ 2つの曲線y=e^x\ および\ y=ax²\ の両方に接する直線の本$ $数を求めよ. [東北大]$ $ここで,\ 求める共通接線の本数は,\ の実数解の個数に等しい.}$ \ 共通接線の方程式を求めるには,\ {両方の曲線の接線の方程式を求めてその一致条件を考える.} 接点が不明なので,\ それぞれの接点を文字でおいて接線の方程式を作成する. 接線y=ax+bと接線y=cx+dが一致する条件は,\ a=cかつb=dである. この2式を両方とも満たす必要があるから連立する.\ 消去が容易なtを消去する. すると{sについての方程式}が得られるから,\ 定数aを分離する. {の実数解1個に対し,\ よりtも1個存在し,\ すなわち対応する共通接線が1本存在する.} よって,\ の実数解の個数を調べることで,\ 共通接線の本数が求まることになる. 後はy=f(s)のグラフを図示してy=aとの共有点の個数を読み取るだけである. 定義域を確認し(分母0),\ さらに極限も調べた上で図示する.\ 後は,\ a0に注意して答える. $,\ より e^s=4a(s-1)}$ $y=4a(s-1)は点(1,\ 0)を通る傾き4aの直線}である.$ $ゆえに,\ 点(1,\ 0)を通るy=e^sの接線の方程式は $ここで,\ 求める共通接線の本数は,\ の実数解の個数に等しい.}$ 本問は,\ 定数aの分離よりも,\ のようにして{基本関数e^sと直線の共有点に帰着}させるのがよい. y=4a(s-1)は,\ s=1のときaの値によらずy=0となるから,\ 常に点(1,\ 0)を通る直線である. よって,\ {点(1,\ 0)を中心に直線の傾き4aを変えて共有点の個数の変化を読み取る}ことになる. y=e^s\ と\ y=4a(s-1)\ が接するときが境目となるから,\ このときの傾き4aを求める. 接点の座標を文字でおいて接線の方程式を作成し,\ (1,\ 0)を通る条件を考えればよい. 傾き4a=e²のときに接する(1個)ことがわかる.\ さらに傾きが大きくなると2個の共有点をもつ. 接線の傾きよりも小さく,\ かつ正の傾きならば共有点なし,\ 負の傾きならば1個の共有点をもつ.

