3直線\ $x+y-4=0,\ 2x-y+1=0,\ 3x-ay-a=0$\ が三角形を作らないような定数
$a$の値を求めよ. \\
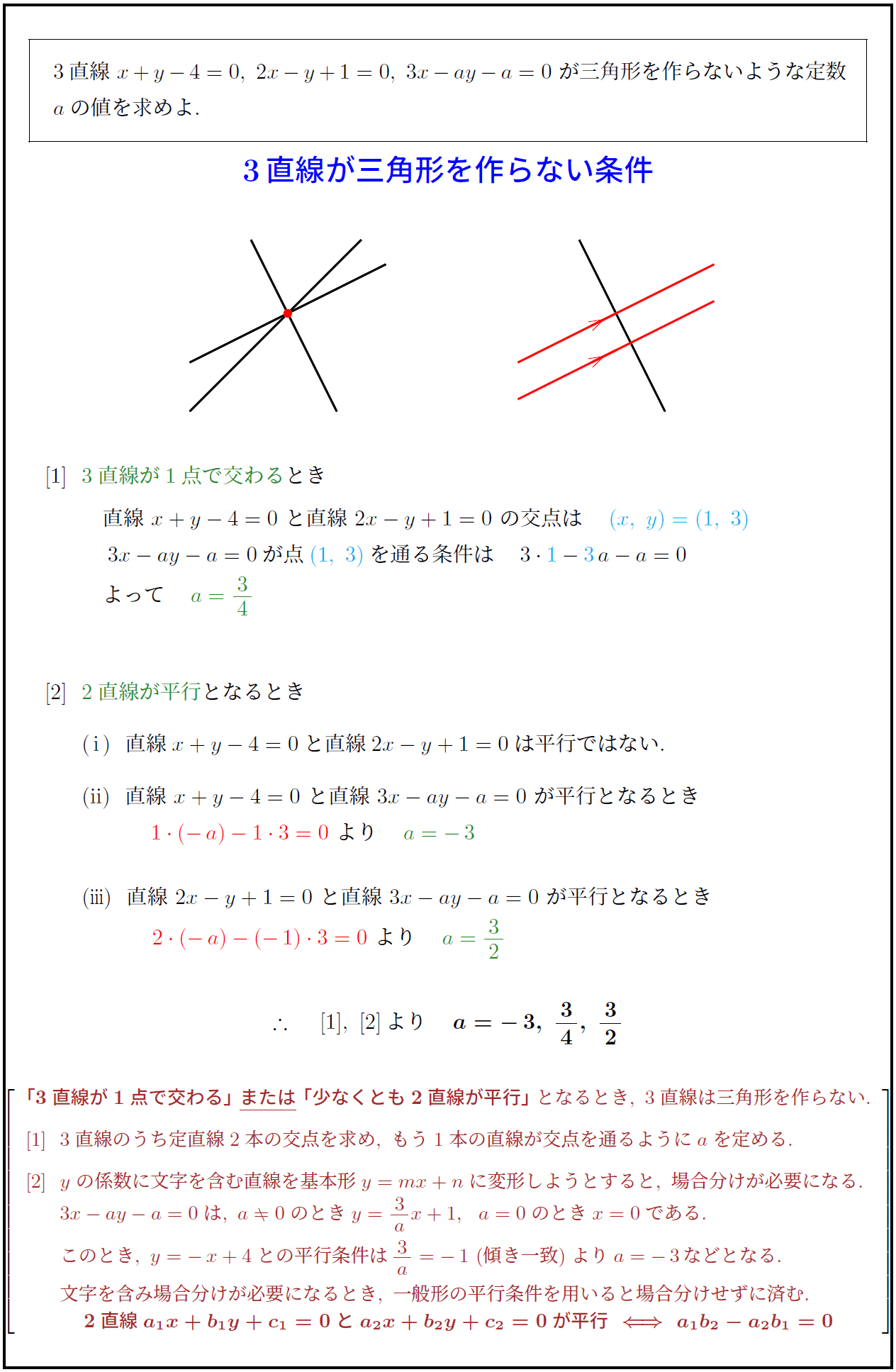
3直線が三角形を作らない条件3直線が1点で交わる}とき
$[1]$}\ \ 直線\ $x+y-4=0\ と直線\ 2x-y+1=0\ の交点は (x,\ y)=(1,\ 3)}$
$[1]$}\ \ $3x-ay-a=0が点(1,\ 3)}を通る条件は
$[2]$\ \ 2直線が平行}となるとき\ 直線$x+y-4=0$と直線$2x-y+1=0$は平行ではない.
$[1]$}\ \ (ii)\ \ 直線\ $x+y-4=0\ と直線\ 3x-ay-a=0$\ が平行となるとき 直線\ $2x-y+1=0\ と直線\ 3x-ay-a=0$\ が平行となるとき \
「3直線が1点で交わる」\ または}\ 「少なくとも2直線が平行」}となるとき,\ 3直線は三角形を作らない.
[1]\ \ 3直線のうち定直線2本の交点を求め,\ もう1本の直線が交点を通るようにaを定める.
[2]\ \ yの係数に文字を含む直線を基本形y=mx+nに変形しようとすると,\ 場合分けが必要になる.
\ \ 3x-ay-a=0は,\ a≠0のときy=3ax+1,\ \ a=0のときx=0である.
\ \ このとき,\ y=-\,x+4との平行条件は\,3a=-\,1\ (傾き一致)よりa=-\,3\,などとなる.
\ \ 文字を含み場合分けが必要になるとき,\ 一般形の平行条件を用いると場合分けせずに済む.
\ \ 2直線a_1x+b_1y+c_1=0とa_2x+b_2y+c_2=0が平行\ ⇔\ a_1b_2-a_2b_1=0}

