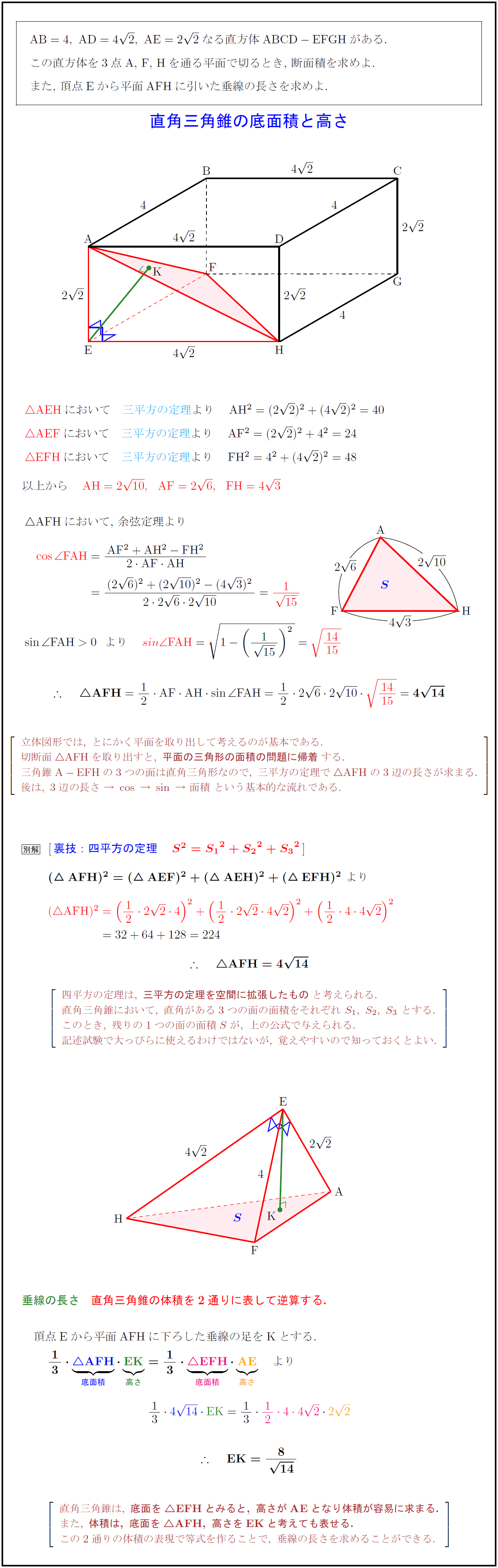
この直方体を3点A,\ F,\ Hを通る平面で切るとき,\ 断面積を求めよ. また,\ 頂点Eから平面AFHに引いた垂線の長さを求めよ. 切断面{AFH}を取り出すと,\ {平面の三角形の面積の問題に帰着}する. 三角形の面積を求めるには,\ まず3辺の長さを求めればよい. 三角錐{A-EFH}について考える. 3つの面は直角三角形なので,\ 三平方の定理で{ AFH}の3辺の長さが求まる. 後は,\ 「3辺の長さ\ →\ cos\ →\ sin\ →\ 面積」という基本パターンである. 裏技「四平方の定理」 ${S²={S₁}²+{S₂}²+{S₃}²$ $(△AFH)²=(△AEF)² + (△AEH)² + (△EFH)²} 四平方の定理は,\ {三平方の定理を空間に拡張したもの}と考えられる. 直角三角錐において,\ 直角がある3つの面の面積をそれぞれ\ S₁,\ S₂,\ S₃\ とする. このとき,\ 残りの1つの面の面積Sが,\ 上の公式で与えられる. 記述試験で大っぴらに使えるわけではないが,\ 覚えやすいので知っておくとよい. {直角三角錐の体積を2通りに表して逆算する. 頂点Eから平面AFHに下ろした垂線の足をKとする. 底面積 直角三角錐は,\ {底面を{EFH}とみると,\ 高さが{AE}となり,\ 体積が容易に求まる.} また,\ {体積は,\ 底面を{AFH},\ 高さを{EK}と考えても表せる.} この2通りの体積の表現で等式を作ることで,\ 垂線の長さを求めることができる.

