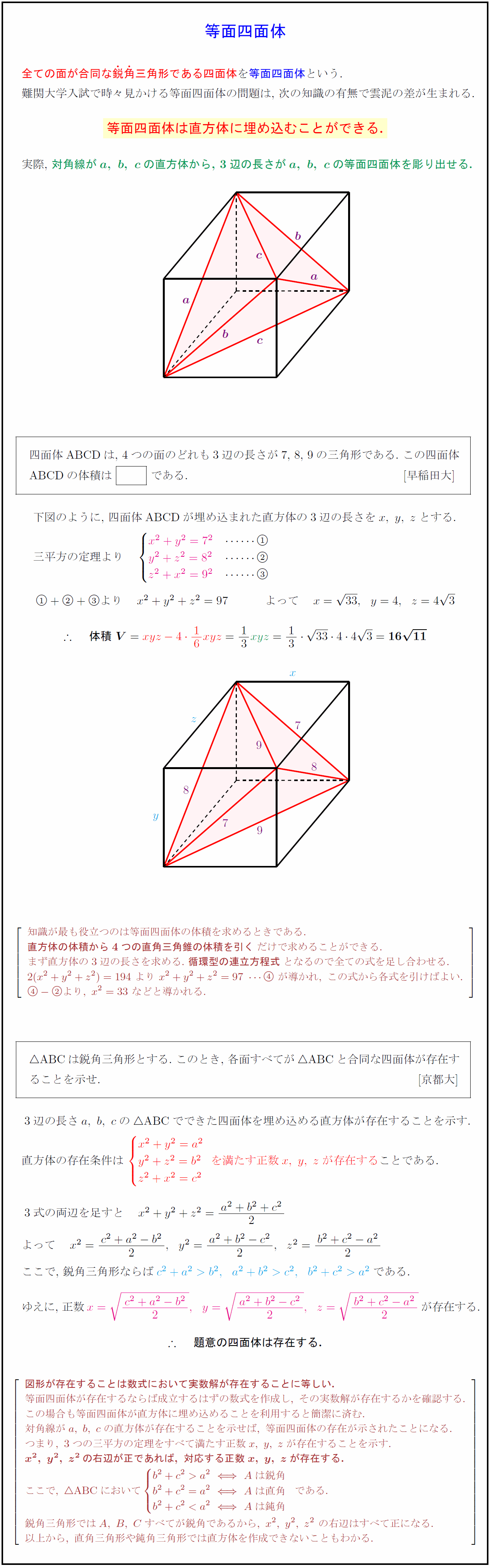
全ての面が合同な鋭角三角形である四面体を等面四面体という. 難関大学入試で時々見かける等面四面体の問題は,\ 次の知識の有無で雲泥の差が生まれる.等面四面体は直方体に埋め込むことができる.} 実際,\ 対角線が${a,\ b,\ c}$の直方体から,\ 3辺の長さが${a,\ b,\ c}$の等面四面体を彫り出せる.四面体ABCDは,\ 4つの面のどれも3辺の長さが7,\ 8,\ 9の三角形である.\ この四面体 ABCDの体積は\ { }\ である. [早稲田大] 下図のように,\ 四面体ABCDが埋め込まれた直方体の3辺の長さを$x,\ y,\ z$とする. 三平方の定理より 知識が最も役立つのは等面四面体の体積を求めるときである. {直方体の体積から4つの直角三角錐の体積を引く}だけで求めることができる. まず直方体の3辺の長さを求める.\ {循環型の連立方程式}となるので全ての式を足し合わせる. 2(x²+y²+z²)=194\ より\ x²+y²+z²=97が導かれ,\ この式から各式を引けばよい. などと導かれる. は鋭角三角形とする.\ このとき,\ 各面すべてが$$ABCと合同な四面体が存在す ることを示せ. [京都大] 3辺の長さ$a,\ b,\ c$の$$ABCでできた四面体を埋め込める直方体が存在することを示す. 直方体の存在条件はを満たす正数$x,\ y,\ z$が存在する}ことである. 3式の両辺を足すと 題意の四面体は存在する.} {図形が存在することは数式において実数解が存在することに等しい.} 等面四面体が存在するならば成立するはずの数式を作成し,\ その実数解が存在するかを確認する. この場合も等面四面体が直方体に埋め込めることを利用すると簡潔に済む. 対角線がa,\ b,\ cの直方体が存在することを示せば,\ 等面四面体の存在が示されたことになる. つまり,\ 3つの三平方の定理をすべて満たす正数x,\ y,\ zが存在することを示す. {x²,\ y²,\ z²の右辺が正であれば,\ 対応する正数x,\ y,\ zが存在する.} 鋭角三角形ではA,\ B,\ Cすべてが鋭角であるから,\ x²,\ y²,\ z²\ の右辺はすべて正になる. 以上から,\ 直角三角形や鈍角三角形では直方体を作成できないこともわかる.

