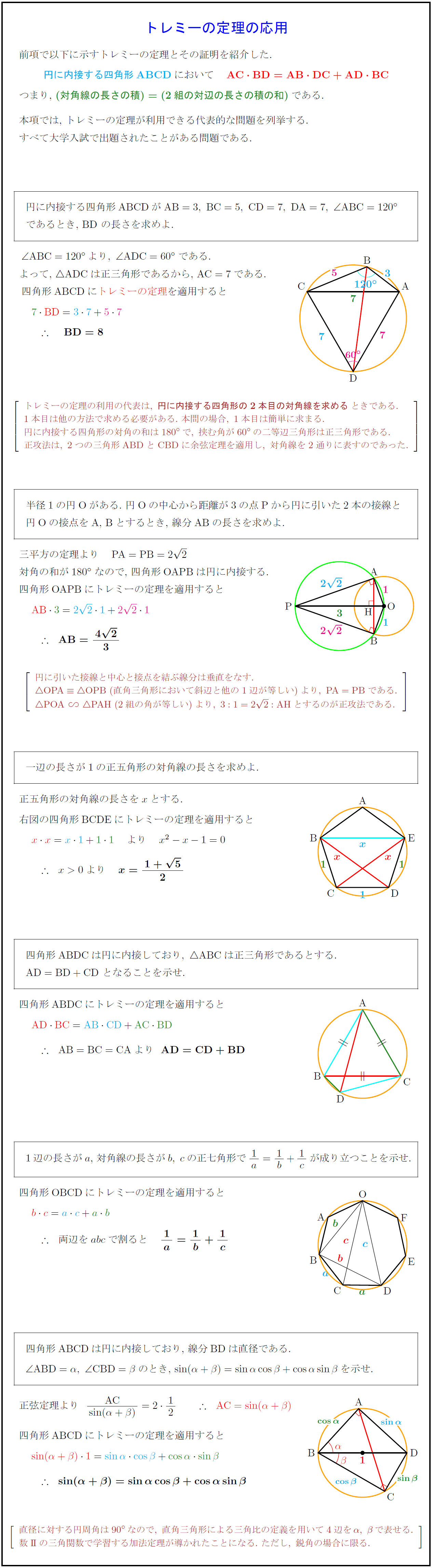
前項で以下に示すトレミーの定理とその証明を紹介した. 円に内接する四角形ABCDにおいて $AC BD=AB DC+AD BC}$} つまり,\ ${(対角線の長さの積)=(2組の対辺の長さの積の和)$である. 本項では,\ 実際にトレミーの定理が利用できる代表的な問題を列挙する. なお,\ 大学入試ではトレミーの定理が役立つ問題をたまに見かける. |} [-.8zh] 円に内接する四角形${ABCD}が{AB=3,\ BC=5,\ CD=7,\ DA=7,\ ∠ ABC=120°}$ であるとき,\ ${BD}\ の長さを求めよ.$ $∠{ABC=120°より,\ ∠ ADC=60°}$である. よって,\ $$ADCは正三角形であるから,\ ${AC=7}$である. ${四角形ABCD}にトレミーの定理}を適用すると$ トレミーの定理の利用の代表は,\ {円に内接する四角形の2本目の対角線を求める}ときである. 1本目は他の方法で求める必要がある.\ 本問の場合,\ 1本目は簡単に求まる. 円に内接する四角形の対角の和は180°で,\ 挟む角が60°の二等辺三角形は正三角形である. 正攻法は,\ 2つの三角形{ABDとCBD}に余弦定理を適用し,\ 対角線を2通りに表すのであった. \半径1の円Oがある.\ 円Oの中心から距離が3の点Pから円に引いた2本の接線と 円Oの接点をA,\ Bとするとき,\ 線分ABの長さを求めよ. \ 三平方の定理より ${PA=PB=22}$ 対角の和が$180°$なので,\ 四角形OAPBは円に内接する. 四角形OAPBにトレミーの定理を適用すると 円に引いた接線と中心と接点を結ぶ線分は垂直をなす. { OPA≡ OPB\ (直角三角形において斜辺と他の1辺が等しい)より,\ PA=PBである.} { POA∽ PAH\ (2組の角が等しい)より,\ 3:1=22:AH}とするのが正攻法である.一辺の長さが1の正五角形の対角線の長さを求めよ. 正五角形の対角線の長さを$x$とする. 右図の四角形BCDEにトレミーの定理を適用すると$ より $x²-x-1=0$ }四角形${ABDC}は円に内接しており,\ { ABC}$は正三角形であるとする. ${AD=BD+CD}\ となることを示せ.$ 四角形ABDCにトレミーの定理を適用すると1辺の長さが$a$,\ 対角線の長さが$b,\ c$の正七角形で$ 1a=1b+1c$が成り立つことを示せ. \ 四角形OBCDにトレミーの定理を適用すると 四角形ABCDは円に内接しており,\ 線分BDは直径である. ${∠ ABD=α,\ ∠ CBD=β}$のとき,\ $sin(α+β)=sinαcosβ+cosαsinβ$を示せ 正弦定理より$AC{sin(α+β)}=212 {AC}=sin(α+β)}$ 四角形ABCDにトレミーの定理を適用すると \ 直径に対する円周角は90°なので,\ 直角三角形による三角比の定義を用いて4辺をα,\ βで表せる. 数II}の三角関数で学習する加法定理が導かれたことになる.\ ただし,\ 鋭角の場合に限る.

