
インターネット上でたびたび話題になるのが次の問題である。

たびたび話題となるのは、答えが1/4派と10/49派に分かれるからである。プログラムを組んでパソコンで繰り返しシミュレーションしてみた人もいた。元はといえば、ある教科書の答えが1/4と間違っていたことが原因で有名になったようである。
「条件付き確率」を知らしめた問題ともされ、その理解なくして正解するのは困難である。
13/52=1/4と答える人は、おそらく最初に引いた時点で確率が決まるため、後から引いた3枚がダイヤであったことは関係ないという考えなのだろう。確かに、最初に箱の中にしまった時点でそのカードがダイヤである確率が1/4であることは疑いようがない。しかし、その後何があっても確率は変化しないとする考え方は合理的なのだろうか。
確率の答えは直感に反することが度々あるが、極端な場合を考えてみたり、感情移入しやすい状況に置き換えて考えてみると理解しやすくなることがある。
確率はもともと賭けから始まった分野である。箱の中のカードのスートが何であるかに100万円賭けると考えると感情移入しやすいだろう。
何としても賭けに勝つためには、できるだけ多くの情報を収集し、それをすべて考慮したうえで未来の事柄の起こりうる割合を考えることが重要である。残りのカードのうち3枚がダイヤであることが判明してもなお、箱の中のカードがダイヤであることに賭けようと思うだろうか。
どう考えても、最初にしまった時点よりも箱の中のカードがダイヤである確率は減っている。
まだ納得いかないならば、超極端な場合も考えてみるとよい。
つまり、残りのカードから13枚を抜きだして13枚すべてがダイヤだったときである。この段階に至ってもなお、箱の中のカードがダイヤであることに賭けようと思えるだろうか。どう考えてもその確率は0であり、そんなものに賭けようものならもはやいいカモである。
実は、確率は情報を得るたびに更新される。これが「条件付き確率」の考え方である。条件付き確率の詳しい説明は最後に載せておいたが、本問を考える上では「確率は情報を得ると更新される」ということだけ認識できていれば十分である。
一方、確率は「最初に抜いた」という順番には左右されない。結局、本問のポイントは「表を見ないで箱にしまった」、つまり「何の情報も得ていない」ことである。情報を得ていないという点では、最初にしまった1枚は残りの48枚と何も変わらず、完全に対等である。
そして、本問で問われているのは、「残りのカードのうち3枚がダイヤである」という情報を得た時点での箱の中のカードがダイヤである確率である。
スートが未知のカード49枚の内ダイヤのカードは10枚あるから、求める確率は10/49である。
先程の超極端な条件になるまでの確率をすべて示すと以下のようになる。ダイヤが出るにつれてどんどん箱の中のカードがダイヤである確率は減少していき、13枚のダイヤが出た時点で0になる。
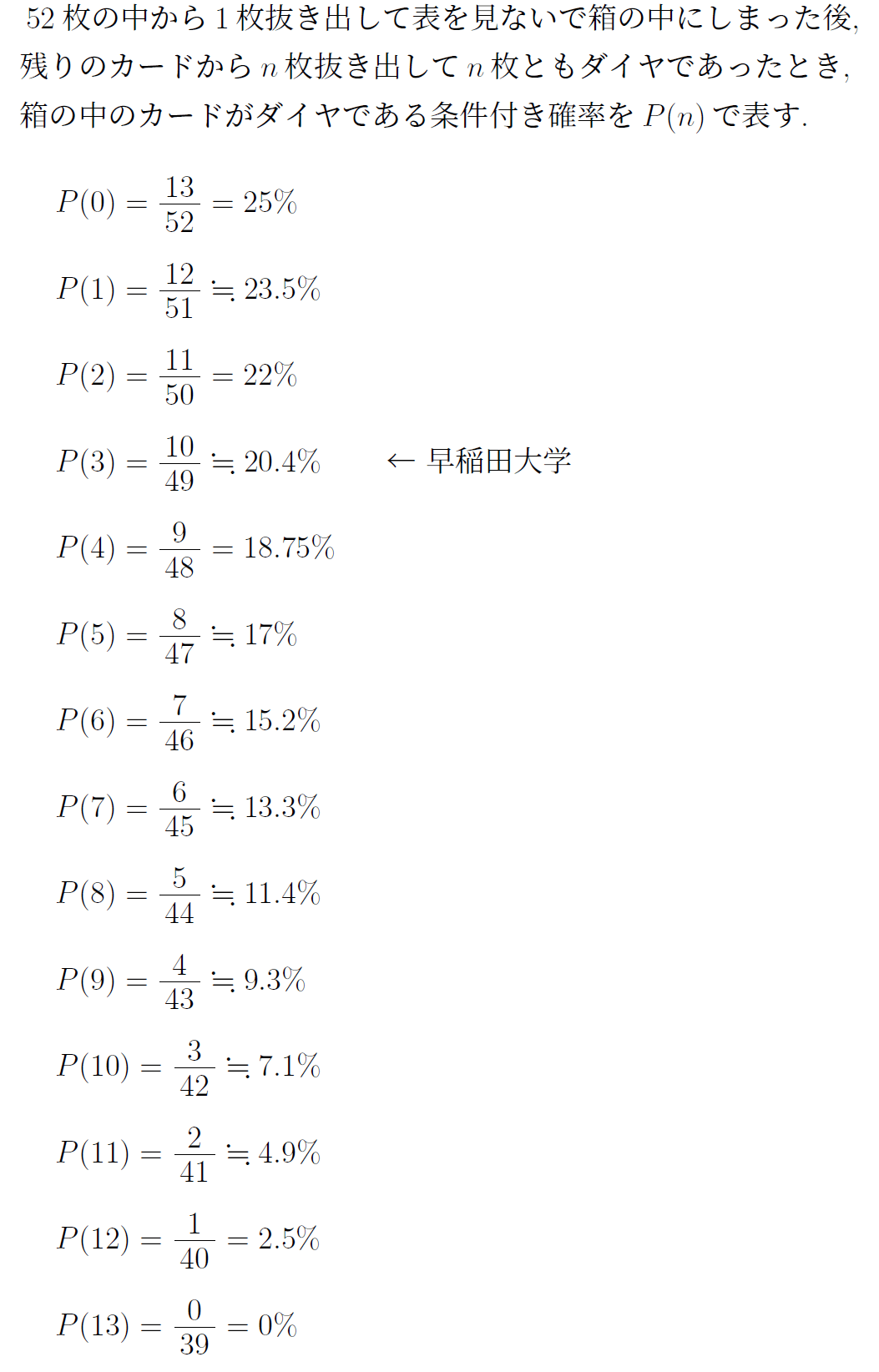
条件付き確率とは
一応、条件付き確率のやや詳しい解説を載せておく。条件付き確率をすでに知っている場合は読み飛ばしてもらって構わない。



条件付き確率については以下の記事もどうぞ。


