
大阪大学では、2013年から前期日程を「一般枠」と「挑戦枠」に分けて募集するという新たな選抜方法が始まった。
「挑戦枠」では、1日目に「一般枠」と同じ試験、2日目に専門数学の試験が行われる。専門数学は、大問2個で180分300点満点である。
そして、初めての「挑戦枠」の専門数学の第2問で、「難易度の高い数学の試験を課して粘り強く考察できる学生を獲得する」という挑戦枠の目的にふさわしい問題が出題された。

「円周率を小数第3位まで特定しよう」という趣旨はわかりやすいが、2003年の東大の問題と比べて非常に厳しい評価が要求されており、問題の√3の小数第7位までの評価をみた時点ですでに嫌な予感しかしない。
下に解答を簡単に示した。(1)はライプニッツ級数に関する頻出パターン問題を学習していれば方針を迷うことはないだろう。
問題は(2)である。不等式で評価するだけなので、発想や手順自体が根本的に難しいわけではない。
しかし、案の定嫌な予感が的中することになる。

「もうやめて・・・・・・」と言いたくなる数値計算である。非常にシビアな評価になるため、少しでも途中計算を間違えると正しい結果が得られない。まあ、自分は電卓の力を借りたわけだが(笑)。
思考力というよりも、「精神力」「持久力」「忍耐力」が問われている。もちろん、単純な計算力やうまく工夫して見通しをよくする先見性や正確さなども必要である。ただ、時間的な余裕はあるので、落ち着いて一歩ずつ確実に歩んでいけば答案を完成させることは難しくない。
この年、挑戦枠での合格者は1名のみであった。また、挑戦枠は2017年度から廃止された。
数学者ルドルフの伝説的偉業
人類は円周率の小数以下を求め続けてきた。
長い間、円周と内接・外接する正多角形の周の長さを比較することで円周率を評価してきた。2003年の東京大学の伝説の問題では、無誘導なのでこの手法に頼らざるを得なかった。
しかし、周の長さの比較で高い精度の円周率を得ることは容易ではない。この問題と同じレベル、たった小数第3位までの評価であっても正160角形が必要である。
紀元前3世紀頃、アルキメデスは正96角形を用いて 3.14084<π<3.14286 を示した。これは3.14までを正しく評価したことを意味する。
この方法は1600年頃の数学者ルドルフ・ファン・コーレン(ドイツ;1540-1610)まで続いた。
ルドルフは、正262角形(正461京1686兆184億2738万7904角形)を用いて、一生をかけて小数以下35桁を正しく評価した。
1610年12月31日にオランダのライデンでこの世を去ったルドルフだが(享年70)、ライデンにある以下の墓石には「3.14159265358979323846264338327950288・・・」が刻まれている。ドイツでは円周率のことをルドルフ数とも呼ぶという。

A.L. Boon, CC BY-SA 3.0, via Wikimedia Commons
17世紀頃になると、微分積分が登場し、収束が速い無限級数を用いた評価が主流となる。
本項の大阪大学の問題は、無限級数を用いると手計算でも小数第3位程度までならば割と容易に評価できることを示している。手計算による方法は、1946年の電子計算機による方法が登場するまで続いた。
以降、計算機の発達に伴って飛躍的に記録が伸び続けており、日本人も大きく貢献している。
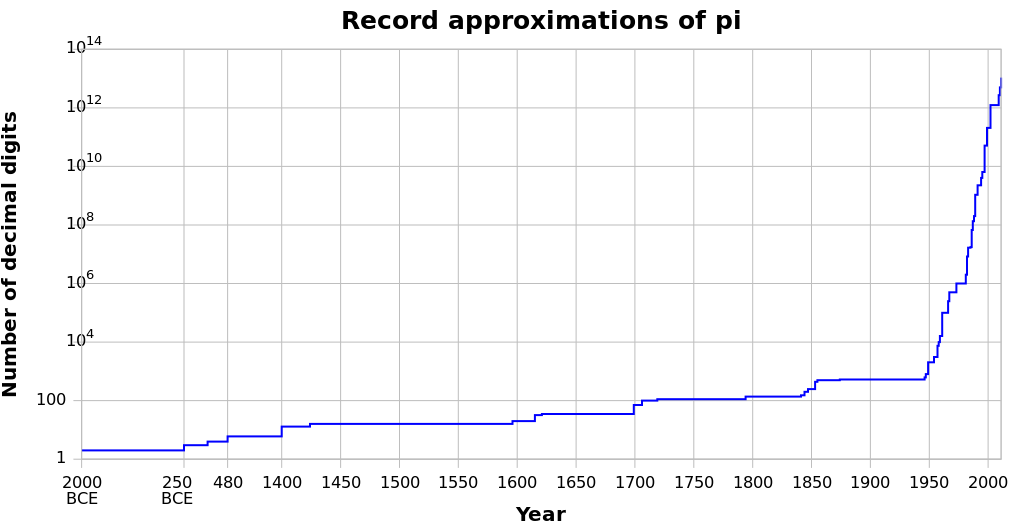
Nageh, CC BY-SA 3.0, via Wikimedia Commons
2022年6月9日、Googleの日本人技術者岩尾エマはるか(筑波大卒)が158日をかけて100兆(=1014)桁まで計算したと発表した。使用したストレージは515TBであった。
概ね10年で1桁増える傾向にあるようで、10年後には1000兆桁になっているのかもしれない。
最新情報は 円周率の歴史(Wikipedia) へ。
計算機のない時代、数学者達は想像を絶する量の計算を強いられた。それに比べれば、この問題の計算はお遊びにもならない。数学研究にはセンスだけではなく「精神力」「持久力」「忍耐力」も必要であるが故、受験生に対してもそれを求めたいということだったのではないだろうか。


