当ページには大学入学共通テスト(旧センター試験)過去問のネタバレ(問題と解答)がかなり含まれています。
過去問演習を行う前にネタバレを見てしまうと過去問演習の意味合いが半減してしまいます。
受験生は各自適切なタイミングで閲覧してください。
問題を解いた直後に閲覧するとリアリティが増すかも?
2011年ⅠA65.95点、2012年ⅠA69.97点と2年連続でかなり簡単な年が続き、難化が危惧された2013年センター試験ⅠA、第1問と第2問は標準難易度だったが、第3問でついに牙をむいた。
その問題が以下である。
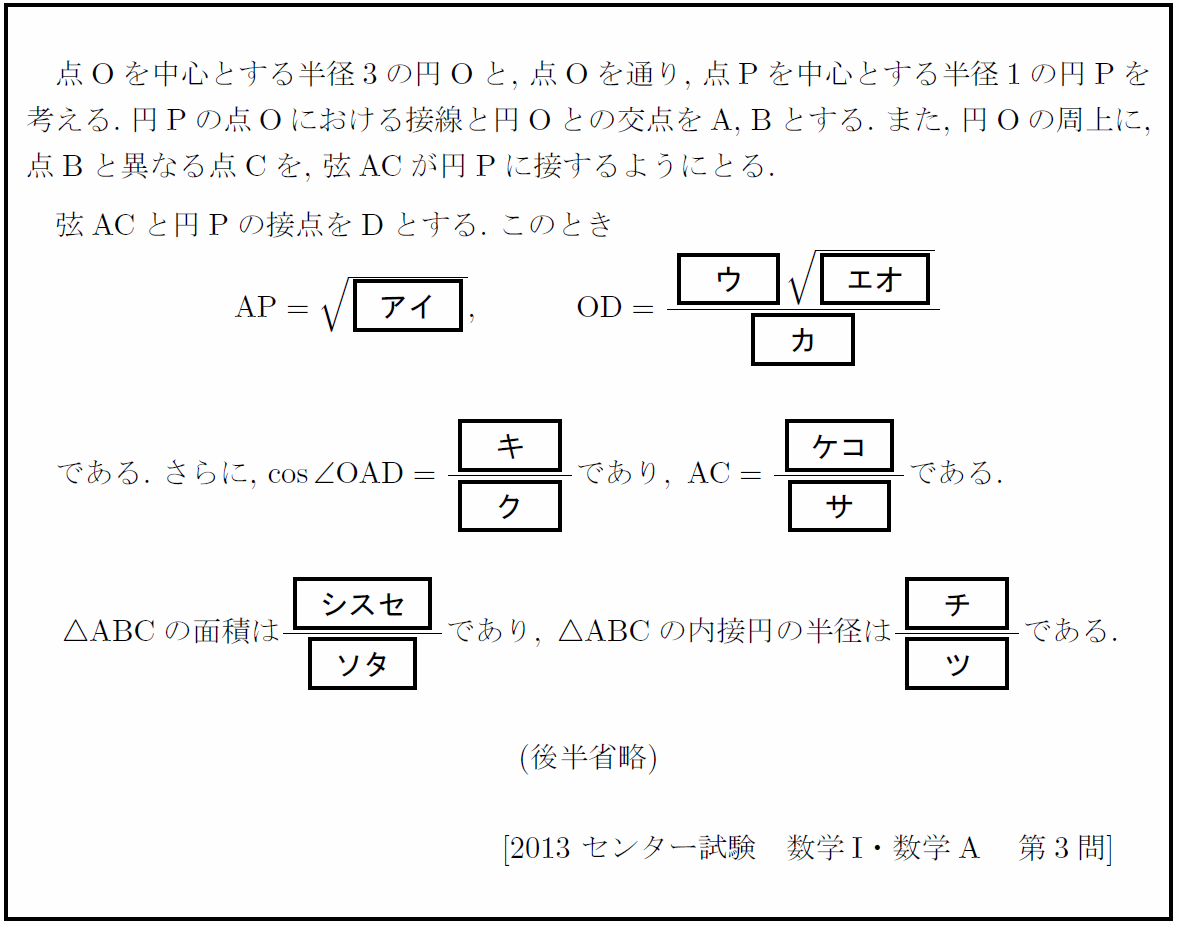
この問題の図を描いてみると下のようになる。
APの長さは三平方の定理ですぐに求まる。問題は次のODの長さである。
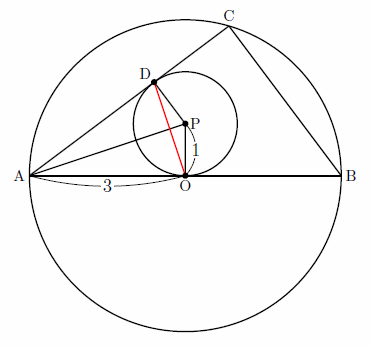
この外部の点から円に接線を引いたときの2つの接点間の長さは、直角三角形の相似を利用するか面積を2通りに表して求めるのが普通で、問題作成者もそれを想定していたであろう。これらは中学図形ではよく使う方法であり、中学生にとっては普通である(というよりこれしかできない)。
しかし、高校生にとっては中学図形の方法は逆に盲点となる。
高校生が普通に受験勉強やセンター対策をしていても使う機会がほとんどない方法であり、尋常ではない数の受験生が求めることができなかった。並以下の学生と文系はほぼ壊滅である。円に内接する四角形の利用、2倍角の公式の利用、トレミーの定理(裏技)の利用、座標平面の利用など、実は他にも様々な解法があるのだが、相応の訓練をしていなければその発想に至るのは難しいだろう。
この大問が真に恐ろしいのは、その後に続く問題が全てODの長さを起点としていることである。
つまり、ODの長さを求めることができなければ、APの長さ(3点)以外が全滅し27点もの大量失点がほぼ確定してしまうのである。しかも、その後は少なくとも内接円の半径までは基本問題であることが明らかで、ODの長さが求まれば容易に解答できるはずである。
受験生は本番中、「ODさえ求まれば後はいけるのに・・・ODさえ・・・ODさえ・・・ODODOD・・・ああああああああああ」とうなされていたことだろう。
このような問題では真の数学力が問われることになる。
国立2次記述試験対策の演習(パターンではない問題を思考力で解く訓練)をしっかり積んできている理系ならば1つの方法で求めることが出来なくても先に述べたような他の方法でその場をしのぐことも可能である。しかし、小手先のセンター対策やパターン問題演習だけでマーク模試で点をとってきたような文系や並レベルの受験生にとっては対応が難しく、点数にも精神にも大きなダメージを受けた。
高校では幾何の問題をいかにひらめきなく座標平面やベクトルで機械的に解くかに重点を置いて学習する。よって、高校生はとにかく幾何に弱い。
もし、本問が数ⅡBで座標平面の問題として出題されたならば、多くの受験生は普通に解くことができたであろう。しかし、数IAで出題され、あろうことか幾何的解法に強制的に誘導された結果、その演習をほとんど行っていなかった多くの受験生が壊滅してしまったのである。
このように、場合によっては不得意な解法に強制的に誘導されることがセンター試験の恐ろしさの1つである。
本問を正攻法で解くことができた学生の多くは、中学生の時から数学が得意だった理系学生である。ハイレベルな理系学生は中学生の時に十分な幾何的考察の演習を積んできており、仮に高校で重点的に学習していなかったとしても中学生の時の勘が失われておらず、このような問題にも容易に対応できる。
しかし、並以下の学生や文系学生は中学生の時に幾何的考察から逃げてきた人が少なくない。「合同の証明問題は難しいから捨てよう」「(ちょっと考えただけで)ここの角度わからない、もういいや」などといった具合に。このような学生には、中学生の時にためにためたツケが大学受験という人生の一大分岐点において回ってくることになったのである。
その日の内に2ちゃんねるでは次のようなAAが広まった。埋めれたのはアイの10だけで、第3問の残りを全て白紙にせざるを得なかった受験生の悲惨な答案用紙を再現したものである。

そして、27点が奪われたショックもさめやらぬままに受けた数ⅡBでは、三角関数が消えて図形と方程式となっていたり、ベクトルと三角関数が融合していたり、まさかの数学的帰納法が出題されたりという傾向変化に多くの受験生が翻弄された。
この年、数IAの平均点は51.20で、2012年の69.97点から20点近くも下げた。その主要因がこの問題であったことは疑いようがない。また、第3問以外もそこそこ厄介な問題であった。さらに、国語が過去最悪の難度で、特に文系は2010年をも下回る過去最低の総合点となった。
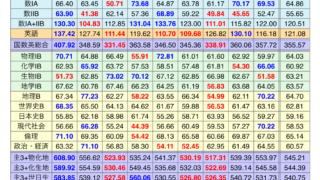
センター試験の平均点推移は次のページへ(当サイト)。