当ページには大学入学共通テスト(旧センター試験)過去問のネタバレ(問題と解答)がかなり含まれています。
過去問演習を行う前にネタバレを見てしまうと過去問演習の意味合いが半減してしまいます。
受験生は各自適切なタイミングで閲覧してください。
問題を解いた直後に閲覧するとリアリティが増すかも?
2010年のセンター数学で起こった惨劇を順を追ってみていく。
外部模試や過去問の傾向から、受験生はⅠAは簡単でⅡBが難しいと予想してセンター試験に挑む。第1問と第2問は普通の問題であった。
受験生は「模試や過去問と同じだ。この調子でいけば高得点確実。」と考えていただろう。
しかし、第3問でその期待は見事に裏切られた。「ⅠAならできる」というおごりから難問に出会ったときの心構えが出来ておらず、パニックを起こしてしまった。その問題が次である。
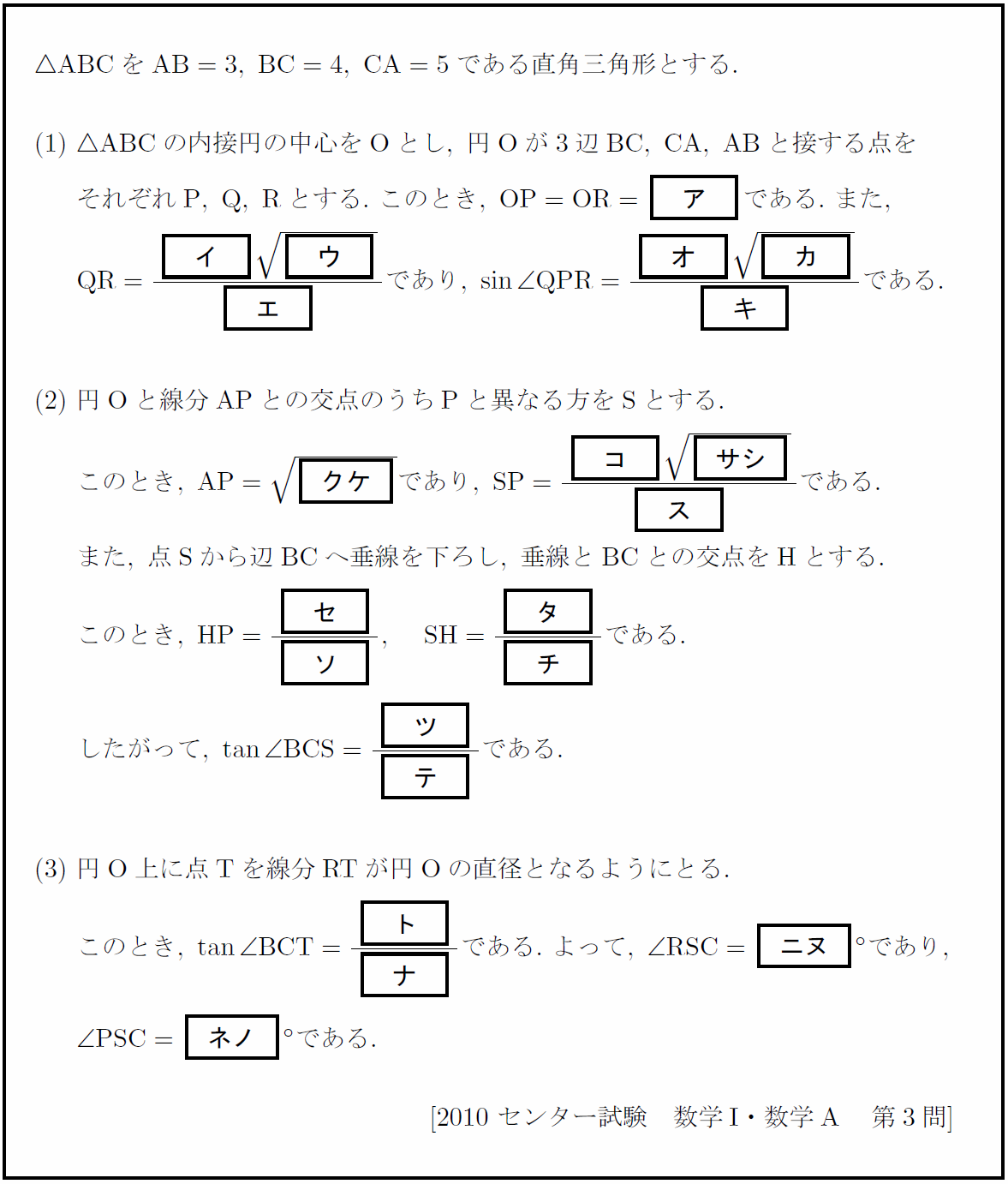
センター試験レベルでは難問である。難しさの1つは、非常に複雑な構図でどこに着目してよいかがわかりにくいところにある。
実際にこの問題で描く図を下に示した。この図は本問で必要な点や線を全て1つの図に描き入れたものなので、最初からこの複雑さで解くわけではないが、この中から適切な部分に着目して解いていくことを15分程度で行うのはあまりに厳しい。
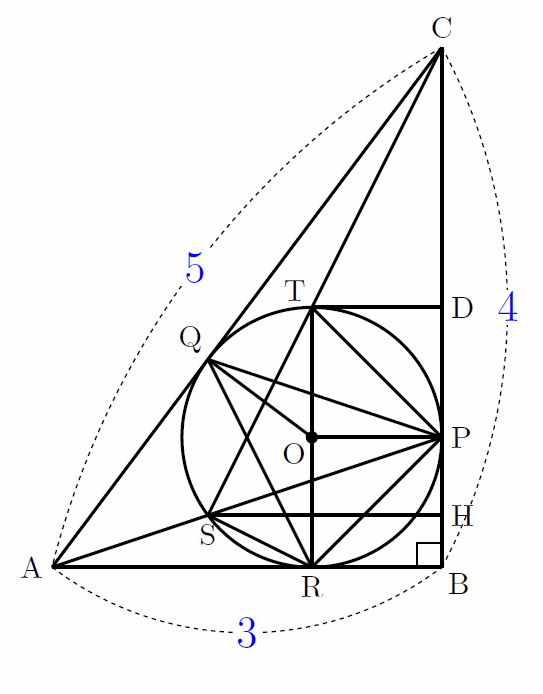
内接円の半径OP、ORの長さは簡単だ。しかし、直後のQRの長さで行き詰まりやすい。「直角三角形の三角比の定義からcosAの値がわかり、あとは余弦定理を使うだけ」というのは言われれば単純だが、一旦パニックになるともう気付けない。パニックのあまり直角三角形の角度が30°、60°、90°であると思いこんでしまった受験生もいたようである。
QRの長さをクリアしても次の難関がSPの長さである。これも言われれば方べきの定理を使うだけだが、複雑な構図の解明に意識が奪われ方べきの定理が思考の彼方にいってしまった受験生が多かった。
受験生は、早々にこの問題に見切りをつけて確率の問題に着手することにした。しかし、本当の地獄はここからだった。
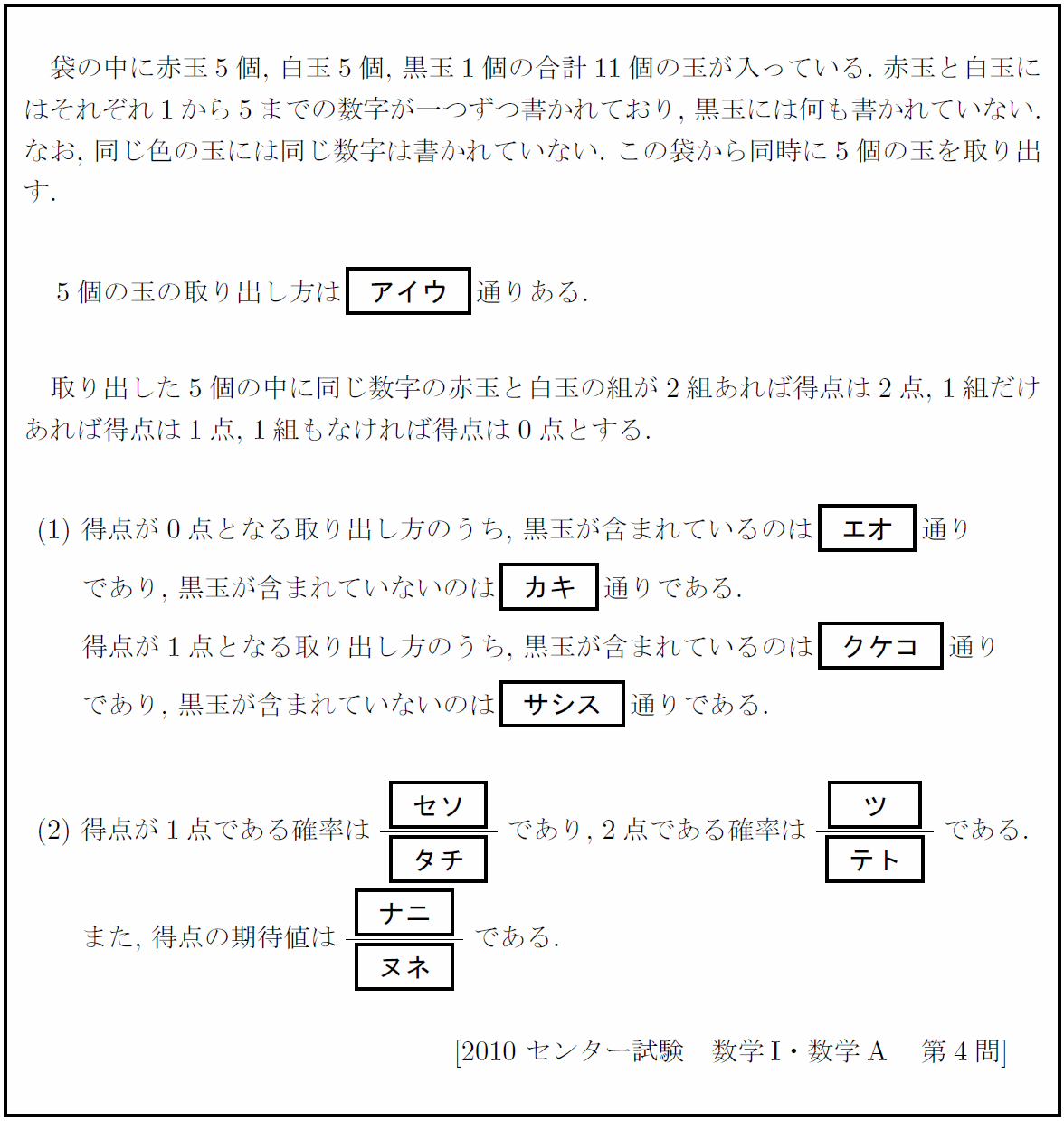
アイウは簡単だ。しかし、その後が難しい。
色と数字の両方を考慮する必要があり単純ではないのだ。「円順列だ」「反復試行だ」などというパターン問題ではなく、「題意を把握してそれをもとに自分で考えることができるか」という思考力が問われている。
2次試験レベルの演習を積み、場合の数の考え方に習熟している人が落ち着いて対応しなければなかなか答えにはたどり着けないだろう。しかも、制限時間は15分ほどしかない。第3問ですでにパニックになっている状態で、この問題を15分程度で解くことを要求されるのは厳しいものがある。
このとき受験生は初めて自分がおかれている危機的な状況に気付いた。大問2つ(55点分)がほとんど埋めれないのである。
「もう一度図形に戻ろう」「いや、やっぱり確率に」「あれ、なんで?」「一旦落ち着こう」「何か見落としているのか?」「これセンターだぞ」「やべえぞこれ」「どうすればいいんだ」「もう時間がないぞ」「このまま終わったらよくても60点だぞ」「神様、ヒントを・・・」「嘘だろおい」「こんな馬鹿な」「頼む、ひらめいてくれ」「くっそおおおおおおおお」という恐怖にも似た受験生の心の声が聞こえてくるようである。
ただでさえ難しい問題である。パニック状況でさらには厳しい時間制限の中でのあせりも生まれもはや為す術もない。他の科目とは違い、数学は終わった時点で自分の点数がほぼ予想できる。多くの受験生はほとんど白紙状態である自分の答案を前に放心状態になっていただろう。数学が終わった直後、あるいは次の日の学校での採点の際に泣いていた女子学生も多かったと聞く。また、ある高校では「みんな悪かったので気にしすぎないように」などという校内放送が流れたとか・・・
本番で数学の問題が解けないときの恐怖は味わったものにしかわからない。自然と手が震え涙が出てくるのである。
高学歴芸人のロザン宇治原氏(京都大学法学部現役合格・京大模試全国2位・センター試験719/800点)は、センター数学で200点取るつもりで挑んだが、30点の大問が解けずに焦ったあまり失神して保健室に運ばれた結果170点だったということをよくネタにしている。芸人ゆえどこまでが真実かは不明だが、数学が得意な人はその状況に現実味を感じることができるのではないだろうか。
直前の模試で90点だったが本番で30点という受験生も少なくなかったようだ。他の科目では考えられない事態である。
確かに第3・4問は難しかったが、解けるはずの部分を確実に取っていれば30点という結果で終わるはずがない。パニックになった結果、冷静であれば取れるはずのところでも失点を重ねてしまったのである。
大問2つが難問であったことがより悲劇を増大させた。もし、難問が1つだけだったならば、他の問題を全て終えた後で最後に難問を粘ればよいだけの話である。しかし、難問が2つだったせいで、図形と確率のどちらにも集中することができず、無意味に往復し続けた挙げ句結局何もできないまま壊滅してしまった受験生が多かったのである。
ところで、「センター試験が難化しても平均点が下がるだけで合否にはあまり影響しないのではないか」と単純には思える。しかし、実際には受験生それぞれ様々な事情があるために多大な影響を受ける。最高難度のIAに影響された2人の現役受験生(富山大学志望)の例を示そう。
男子学生(理系) マーク模試(1ヶ月前) 数学140/200点 「160点を目指すぞ(`・ω・´)」
女子学生(文系) マーク模試(1ヶ月前) 数学40/200点、国語185/200点 「ううう・・・数学・・・(´;ω;`)」
1ヶ月前、2人の学生の数学力には100点分の差があった。男子学生は普通に最後の追い込み、女子学生は教師に「どうせ全部は解けないんだから基本問題だけでもなんとか確保しろ」と言われたとおりに基本パターンの習得に全力を費やした。
センター試験(数学)の結果が出る。
男子学生「数学108/200点。ううう・・・数学・・・(´;ω;`)」
女子学生「数学92/200点。やったよーーー(`・ω・´)」
1ヶ月前にあった100点差はわずか16点差にまで縮まった。男子学生は得意科目で高得点を取ろうと意気込んで挑んだものの、逆に焦りを生み自滅した。一方、女子学生は例年に比べて高難度であることに気付くことすらできなかった。彼女にとっては今までの模試と何ら変わらなかったのだ。変に焦ることもなく、「捨てるべき問題を捨て、取るべき問題を取る」を着実に行った結果、実力通りの点数を獲得できたのである。自己採点直後は「あれ?なんか周りの雰囲気暗いんだけど・・・」と狐につままれたような気分だっただろう。
なお、女子学生は本番では92点であったが、直前の過去問演習では106/200点を記録した年もあった。単純に基本パターンを習得するだけではなく、実際の過去問を用いた時間配分の練習なども含め、かなり戦略的にセンター対策を行った結果である。
センター試験は所詮穴埋めである。正しく対策したならば1ヶ月で40(2割)→106(約5割)というのもさほど難しい話ではない。理科や社会ならばもっと容易だろう。また、彼女は決して数学だけに集中していたわけではなく(数学の勉強時間は全体の1/3で1日4時間くらい)、他の科目もきちんと学習しつつの結果である。
センター試験でも2次記述試験でも、最後の1ヶ月間の過ごし方1つで点数は大きく変わる。1ヶ月前の模試の判定はあくまでも参考にすぎないのである。
最終的に、男子学生は不合格となり浪人を選択、女子学生は富山大学に進学した。元々圧倒的な国語力をもっていた女子学生は、苦手な数学で他の受験生に差をつけられなかったためにもはや落ちる要素はなく、難なく2次記述試験も突破できた。最後までぶれずに自身が最低限やるべきことをやった結果、運も味方してくれたというわけである。
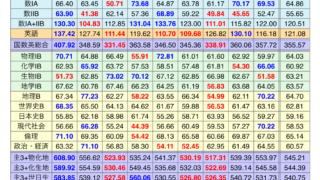
2010年センター数学IAの平均点は48.96点で、2008年の66.31点、2009年の63.96点から大幅に下がった。2次記述試験で難問が出題されて誰も解けなかったということは珍しくない。しかし、30万人以上の受験生が受けるセンター数学IAにおいて繰り広げられた惨劇であるがゆえ伝説となっている。
ちなみに、この年理系で選択者が多い物理の平均点は前年比ー10点、化学の平均点はー15点という悲惨さで、理系の総合点は最低だった。
センター試験の平均点推移は以下のページへ。