
一見では普通の整数問題にすぎないが、本問は伝説の数学者の有名エピソードを背景にもつ。
難易度は低いので(うまくやらないと計算は大変)、数Aの整数を学習済みならば自力で解いてみるとよいだろう。なお、整数分野が明確に高校数学のカリキュラムに組み込まれたのは2012年からなので、2009年当時の受験生には難問である。
解答を示す。
「因数分解して組合せを考える」という整数問題の基本的な解法で求まるが、その前に候補を絞り込んでおかなければかなり計算が面倒である。

これは、1729が2つの正の立方数の和で2通りに表されることを意味している。
本問が意味しているのはここまでだが、さらに以下の表から「2つの正の立方数の和でただ2通りに表すことができる最小の自然数が1729」であることがわかる。
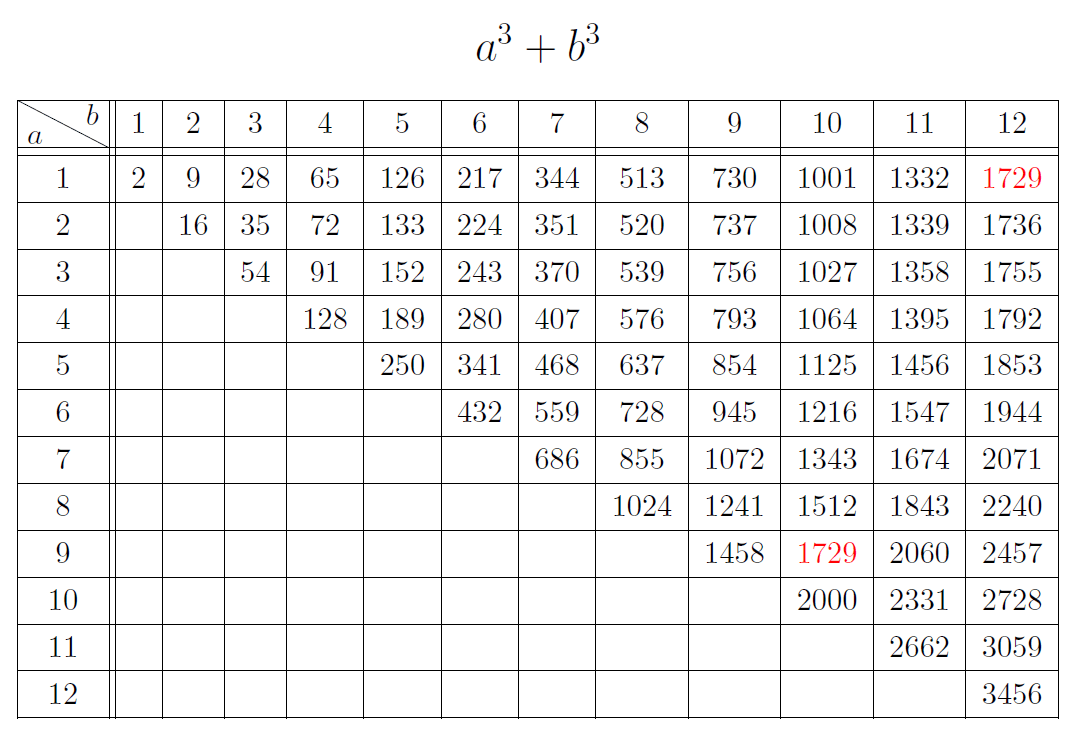
ハーディ・ラマヌジャンのタクシー数
ゴッドフレイ・ハーディ(イギリス)が、療養所に入っていたシュリニヴァーサ・ラマヌジャン(インド ; 1887~1920)の見舞いに行ったとき、「乗ってきたタクシーのナンバーは1729だった。さして特徴のない、つまらない数字だったよ。」と言った。
これを聞いたラマヌジャンは、即座に「そんなことはありません。とても興味深い数字です。それは2つの立方数の和で2通りに表せる最小の数なのです。」と反応してみせた。これは、ラマヌジャンがあらゆる数に興味を持ち、数に対する探究心が非常に高かったことを象徴する逸話である。
これに由来し、「1729」をハーディ・ラマヌジャンのタクシー数という。
インドの魔術師ラマヌジャン

以下のような公式や定理を非常に鋭い直感力で次々と生み出した超天才数学者である。
eは数Ⅲで登場する「自然対数の底」で、e≒2.71である。
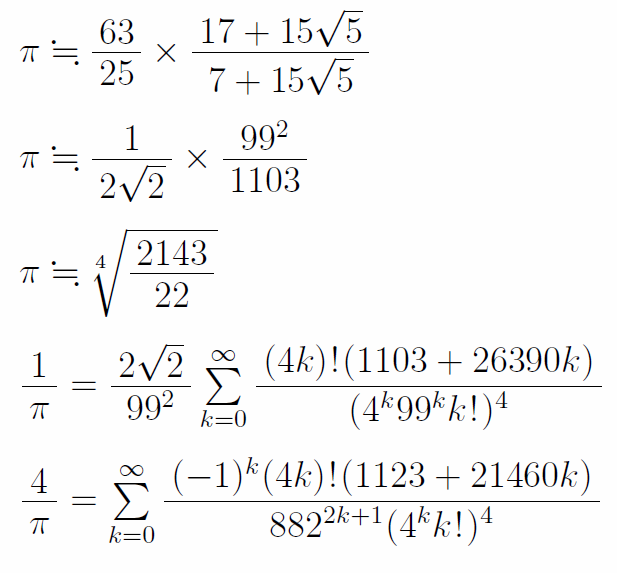

数学者でもいかなる思考過程で得られたのかを辿ることが困難であったため、魔術にもたとえられる。特殊相対性理論はアインシュタインがいなくても誰かが発見しただろうが、ラマヌジャンが見つけた定理の多くはラマヌジャンがいなかったら今でも見つかっていないだろうと述べる数学者もいる。
多くの業績を残したラマヌジャンであったが、正しい数学教育を受けていないために「証明」という概念を知らず、何故そうなるかを説明できなかった。熱心なヒンズー教の教徒であった本人によれば、「ナマギーリ女神が舌の上に書いてくれた」という。彼が26歳までに発見した定理に関してその後多くの数学者の協力で証明が行われたが、その作業が完了したのはラマヌジャンの死後70年以上が経過した1997年のことである。
1887年、ラマヌジャンはインドのカースト制最上級バラモン階級の家庭で生を受けた。しかし、カースト制では身分と貧富は別であり、ラマヌジャンの家庭は極貧であった。教育熱心な母の影響で成績は優秀だったが、15歳のときに「純粋数学要覧」という数学の公式集(証明がなく公式だけ)に出会って以来数学のみに没頭するようになり、大学も退学した。21歳のとき、9歳の娘ジャーナキと結婚した(え!)ラマヌジャンはインドの港湾事務局の職に就いたが、ここでも数学に没頭した。
その後、周囲の勧めを受けて自身の数学的成果を宗主国イギリスの数学者に送る。ほとんど黙殺されたが、「ケンブリッジにハーディあり」とも謳われた大数学者ハーディの目に止まった。ハーディも最初は半信半疑だったものの、精密な調査の結果ラマヌジャンの天才ぶりに気付いたのだ。
ハーディーの強い招致活動により、バラモンの戒律に背いてはいたが、ラマヌジャンは宗主国イギリスに渡ることになった(1914年)。天才と秀才は最高の組合せである。毎朝天才ラマヌジャンが持ってきた5,6個もの定理を秀才ハーディが1日かけて証明した。こうして最高の数学を生み続けていたラマヌジャンであったが、イギリスの風土に馴染むことができず、やがて病魔に襲われ祖国インドに帰国するものの、1920年32歳の若さでその生涯を閉じた。
ラマヌジャンは、32年の短い生涯の内に3254個の定理を発見した。そのうち2/3はラマヌジャンが新しく発見したもの、1/3は既に知られていたがラマヌジャンが独自に再発見したものであった。それらは、円周率の計算やフェルマーの最終定理の証明、宇宙論にも応用されている。
かのハーディは晩年「私の数学上の最大の功績はラマヌジャンの発見だった」と述べている。
ラマヌジャンの生涯が2016年に映画化された。
ラマヌジャンが残した論文やノートを閲覧できるサイト
Srinivasa Ramanujan
また、ラマヌジャンに関する記述は、以下のような書籍やサイトを参考にした。
![奇蹟がくれた数式 [DVD]](https://m.media-amazon.com/images/I/51S8Ucr9OVL._SL160_.jpg)




