

1998年信州大学の問題は、言わずと知れた(?)フェルマーの最終定理の説明から始まっていた。
このことだけでも大学入試では他に例を見ないのだが、問題自体の形式も大学入試では非常に珍しいモノであった。
x3+y3=z3 は成り立たないことがすでに証明されているにもかかわらず、「x3+y3=z3 が仮に成り立つとしたらどうなるかを考察せよ」というのである。
実は、このフェルマーの最終定理が証明される過程において、「もし仮に整数解が存在するとしたら解はどんなものなのか」を追求することで大きな進展があった。これにちなんだ出題といえるかもしれない。
解答を示す。指数部分が2、つまり三平方の定理の形 x2+y2=z2 の場合は整数分野の頻出パターンである。明確に整数分野を学習するようになったのは2013年開始の教育過程からなので、1998年当時の受験生には相当な難問であっただろう。
証明は背理法による。x, y, zが全て3の倍数でないと仮定し、左辺と右辺の余りが一致しないことを示せばよい。
2乗の場合は3で割った余りを考えればよいが、3乗の本問では9で割った余りを考える必要がある。合同式を用いると簡潔な記述になる。

伝説のアマチュア数学者フェルマーの功績と遺言
ピエール・ド・フェルマー(1607-1665;フランス)
17世紀のアマチュア数学者フェルマーの本職は裁判官であった。その傍らで趣味の数学研究に没頭し、世界最高レベルの数学を生み出していた。
フェルマーはひねくれた性格の持ち主で、自分の研究成果を証明をつけずに数学者に送りつけて苦しめるのが好きだった。研究成果をほとんど発表しなかったフェルマーの功績が知られているのは、主にデカルト、メルセンヌ、パスカルといった数学者らとの文通に基づく。
フェルマーの功績は多岐にわたる。パスカル(フランス)と共同で確率論の基礎を創設、デカルト(フランス)とは独立して平面や空間に座標を導入して図形を扱う解析幾何学を構築した。微積分の先駆的研究を行い、現在の微分・積分にかなり近い手法で極大・極小, 接線, 面積を求めた。ニュートンの微分はフェルマーの方法に基づいている。光学においては、光線は伝播時間の合計が最小となる経路を辿るというフェルマーの原理(最小時間の原理)も有名である。
フェルマーの名が知られるようになったのは数論研究においてであり、「数論の父」とも称される。フェルマー数、フェルマーの小定理、無限降下法などは受験数学でも馴染みが深い。
数論研究のきっかけは、1630年代に古代ギリシャの数学者ディオファントスの『算術』に出会ったことであった。フェルマーは、その余白に有名な48の発見を証明なしで書き残した。これらはフェルマーの死後の1670年に息子によって出版され、世に知られるようになった。
このうち47の命題は後の数学者達によって証明または反証が与えられたが、『算術』の問題8の横の余白に記された1つだけ解決できないものが残されたため、これが「フェルマーの最終予想」と呼ばれるようになった。現代風に表すと以下となる。
フェルマーの最終予想
xn+yn=zn
nが3以上の自然数のとき、この等式を満たす正整数x, y, zは存在しない。
x2+y2=z2 を満たす正整数(x, y, z)の組は(3, 4, 5)や(5, 12, 13)など無数に存在することが知られている。ところが、フェルマーによると指数nを3以上にすると解が1つも存在しなくなってしまうというのである。
さらにこの書き込みに続けて、「この定理に関して私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる。」と書き残してあったことが、後世の数学者達を苦しめる元凶となった。
当初は「フェルマーが証明を見つけたといっているのだから、誰かがすぐに証明を発表するだろう」と考えられていたに違いない。命題自体は中学生でも理解でき、そのうち懸賞金も賭けられたため、プロ・アマチュアを問わず多くの数学者が挑戦するようになった。しかし、誰一人証明できないまま、350年以上もの歳月が流れた。実際に証明されたのは、冒頭の問題で示されていたように1995年になってからであった。
繰り返される挫折と悲劇、そして栄光へ。
これは、350年以上の長きに渡って世紀の難問に挑み続けた数学者達の物語である。
初期のアプローチ
長い間、個別のnの場合を証明しようとする試みが続いた。
元々、例えばn=3のときが証明されればn=(3の倍数)のときが証明されたことになるので(x3+y3=z3 が解をもたないならば、x6+y6=z6、つまり (x2)3+(y2)3=(z2)3 も解をもたない)、結局はn=4の場合とn=(素数)の場合を証明すればよいのである。
n=4の場合はフェルマー自身の無限降下法による証明が残っていたが、その次の一歩ですら1世紀もの時間を要した。
1760年になってようやく、18世紀最大の数学者レオンハルト・オイラー(1707-1783;スイス)がn=3の場合を証明した。しかし、オイラーをもってしてもフェルマーの最終予想への貢献はn=3の場合のみに留まった。
さらに半世紀以上経った1823年、ソフィ・ジェルマン(1776-1831;フランス)によって大きな飛躍がもたらされた。
ジェルマンは、それまでの個別的戦略を改め、多くのnの場合をまとめて証明する包括的戦略を試み、「pを2p+1も素数となるような奇素数(ソフィ・ジェルマン素数)とするとき、xp+yp=zp においてx, y, zの少なくとも1つはpの倍数」を証明した(ソフィ・ジェルマンの定理)。「x, y, zの少なくとも1つはpの倍数」は解に対する非常に厳しい制約であり、「pがソフィ・ジェルマン素数のとき自然数x, y, zが存在する可能性は非常に低い」を示したことになる。完全に存在しないことまでの証明には至らなかったが、この戦略はその後の進展に大きく影響した。
ソフィ・ジェルマン(1776-1831)は、フランスの数学者・物理学者・哲学者である。
1776年に裕福な商人の家庭で生を受けたジェルマンは、13歳の時に父の書庫で見つけた『数学史』の中のアルキメデスの最期に興味をもったことで人生が変わった。
アルキメデスが生涯過ごしたシチリア島・シラクサは、紀元前212年ローマ軍の侵略を受けた。ローマ軍の将軍はすでに名が知られていたアルキメデスには危害を加えないよう兵士達に命令していたが、砂地に描いた図形に夢中になっていたアルキメデスはローマ兵に声を掛けられたが無視し、腹を立てた兵士に殺害された。
数学とはそれほどまでに夢中になれる学問なのか・・・
深く感銘を受けたジェルマンは、勉強に没頭し、その生涯で数学・物理学の発展に大きく貢献することになる。
しかし、その学者人生は決して順風満帆なものではなかった。そのたった1つの理由は
女
フランスは特に女性に対して差別的だったのだ。
10代のジェルマンは、夜中まで起きて父の書斎にあった数学の本を読みあさった。数論や微積分学の基礎の独習に加えてラテン語とギリシャ語も独学し、ニュートンやオイラーの本でさえも読めるようになった。両親は数学の勉強に猛反対してロウソクと暖かい洋服を取り上げたが、ジェルマンは毛布にくるまり隠し持ったロウソクで勉強を続けた。
1794年、ジェルマンが18歳の時、パリに最高学府「エコール・ポリテクニーク(高等理工科学校)」が設立されたが入学は男子に限られていたため、以前在籍していた男性の名前ルブランを借りて学校に潜り込んだ。ジェルマンは講義ノートを手に入れ、課題の解答を教員をしていた18世紀最高の数学者の1人であるジョセフ・ルイ・ラグランジュへ送り始めた。しかし、非常に独創的で優れた解答であったためにラグランジュに面会を求められ、正体が暴かれてしまう。幸い、ラグランジュはジェルマンが女性であることを気にせず、彼女のよき指導者となった。
1798年、ジェルマンはルジャンドルの『数の理論』がきっかけで数論に興味を持ち始め、フェルマーの最終予想を知った。数年かけて研究してフェルマー予想の進展を確信したジェルマンは、世界一の数論研究者とされる19世紀最大の数学者カール・フリードリヒ・ガウスに相談することにした。しかし、女を相手にしてくれるか分からない。不安に思ったジェルマンは再びルブランという偽名を用いて1歳年下のガウスへ手紙を出した。ガウスは相手の正体に気付かず、「数論があなたのように優秀な友を得たことを嬉しく思います」と返事したのだった。
1806年、ガウスはナポレオン率いるフランス軍が占領したドイツの都市に住んでいた。ジェルマンはガウスがアルキメデスと同じ運命になることを心配し、家族の友人であったペルネティ将軍にガウスの安全の確保を懇願する内容の手紙を書いた。ペルネティ将軍は提言通りガウスを保護し、「あなたが命拾いしたのはジェルマンのおかげです」と告げたが、ジェルマンを知らなかったガウスは感謝しつつも困惑した。
その出来事から3か月後、ジェルマンは手紙の中で自分の正体をガウスに明かした。ガウスは若い女性であったことに非常に驚きながらも感謝と賞賛に満ちた返信をした。
ガウスとの文通はジェルマンに多くの刺激を与えてくれたが、1808年にガウスがゲッティンゲン大学の天文学教授に任命されてからは興味が数論から応用数学に移り変わり、ガウスは返事をしなくなった。
よき師をなくしたことに落胆したジェルマンは、数学から離れ、物理学に傾倒し始めた。ここでも優れた能力を遺憾なく発揮し、弾性理論の先駆者の1人となり、パリ科学アカデミーから大賞を受賞するまでに至った。
1815年に科学アカデミーがフェルマーの最終予想に対する賞を提案したことをきっかけに数論への興味が再燃し、1823年にソフィ・ジェルマンの定理を発表した。
晩年に再び交流をもったガウスは、ジェルマンに名誉学位を授けるようにゲッティンゲン大学に働きかけたが、生前に実現することはなく、1831年にジェルマンは乳ガンでこの世を去った(55歳)。数学・物理学の発展に多大なる貢献を果たしたにもかかわらず、国の役人は死亡診断書に「数学者」ではなく「年金受給者」と記した。
1889年、パリにそれまでの記録の2倍ほどにもなる世界で最も高い312.3mの巨大建造物が建築された。
エッフェル塔
建築技師達は金属資材の弾性に特別な配慮を要求された。しかし、エッフェル塔に刻まれた72名の学者の中に、弾性理論に大きく貢献したはずの偉大な女性科学者の名前はなかった。
ジェルマンの戦略にのっとり、1825年にディリクレ(ドイツ)とルジャンドル(フランス)がn=5の場合を独立に証明した。
ディリクレは1832年にn=14の場合についても証明した。1840年にラメとルベーグによってn=7の場合が証明されたが、非常に複雑な手法であったために後に続くものが現れず、個別証明の時代は完全に終わった。
1850年頃、エルンスト・クンマー(ドイツ)は「イデアル数」という新たな概念を導入し、nが正則素数であるすべての場合について証明した。さらに、100以下の非正則素数(37, 59, 67のみ)の場合を個別に証明し、n=3~100の場合にはフェルマーの最終予想が成り立つことが明らかになった。
その後の半世紀に大きな進展はなく、20世紀に入ると数学の最先端は他の領域に移り初めた。果敢に立ち向かった懸賞金目的のアマチュア数学者達も多くいたが、プロの数学者達はフェルマー予想に対する興味を失っていった。フェルマー予想は仮に証明できたとしても数学的価値に乏しいと考えられるようになったのである。
証明の必要性
さらに時は流れ第2次世界大戦の終わりを迎えた頃、人間が一生かけてもできない膨大な計算を短時間で行うことが可能になった。
コンピューターの誕生
クンマーは、膨大な計算が必要ではあるが、理論上は非正則素数の場合を個別に解決できることも示していた。そこにコンピュータが誕生して小さいnの場合から次々に解決することが可能になった。
コンピュータによって、1950年頃にはn=500まで証明され、1994年にはn=400万までが証明された。しかし、残念ながら非正則素数は無限にある。仮にコンピュータを用いてあるnまでの場合をすべて証明できたとしても、無限にあるすべての整数nについて証明されることは永遠にないのである。
証明のない予想がどれほど危ういものなのかを示す例をいくつか挙げよう。
33・・・331は素数か

この数列は一見するとずっと素数が続くようにも思えるが、実際に確かめてみると8番目で素数ではないものが出現する。
オイラー予想
レオンハルト・オイラーは、フェルマー予想をさらに拡張した以下の方程式には自然数解がないと予想した(オイラー予想)。
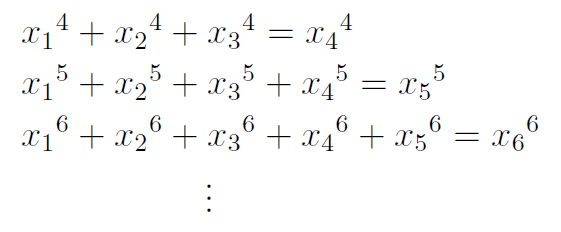
この予想は200年もの間証明もされず反例も見つからなかったので正しい予想であると考えられるようになっていたが、1966年に最初のスーパーコンピュータCDC6600を用いて5乗の場合の反例が発見され、わずか2行の論文でオイラー予想が正しいと信じて証明を試みてきた数学者達の研究のすべてが否定された。
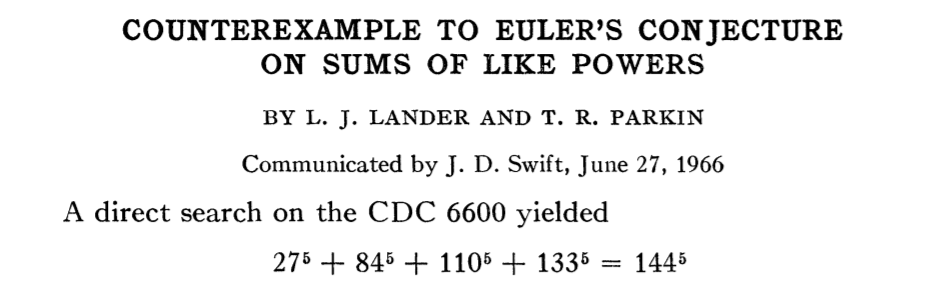
1988年には4乗の反例も発見され、同時に無数の自然数解をもつことまでもが証明された。
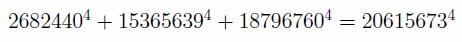
スキューズ数
18世紀末、当時15歳の19世紀最大の数学者カール・フリードリヒ・ガウス(1777-1855;ドイツ)は、素数の分布を予想する式を与えた。この式はかなり正確だったが、常に実際よりもわずかに多めの値が得られた。1兆まで調べても常に多かったので、数学者達はこの傾向が無限に続くと考えていたが、1955年にスキューズ(南アフリカ)が下に示したスキューズ数と呼ばれる数の少し手前で予想を下回ることを示した。

これは想像を絶する大きさの数であり、宇宙に存在する全素粒子数1088個をもってしても比較対象にすらならない。当時は「数学的意味を持つ最大の数」であった。現在はグラハム数のように10進法では記述することすら出来ないほど巨大な数が考察対象となっているようである。
これらの例でわかるように、どんなに大きな値まで調べたとしても、証明されない限りは予想はあくまでも予想にすぎず、いつ何時反例が見つかってもおかしくないのである。
ゲーデルの「不完全性定理」
証明に関しては、もう1つ面白い話がある。
1931年、クルト・ゲーデルが示した「不完全性定理」は数学者達に大きな衝撃を与えた。数学者達は「数学体系は一切の矛盾がない完全なものであり、いかなる命題も真偽が判断できる」ことを当然のように信じて疑っていなかった。
しかし、ゲーデルは「数学が完全ではなく、数学的に証明も反証も出来ない命題が存在する」ことを数学的に証明してしまったのである。これは、有名な嘘つきのパラドックス「私は嘘つきだ」を焼き直した次の命題でたとえられる。
「この命題は証明できない」
もしこの命題が偽だとすると証明できることになるが、証明できないというこの命題自身に矛盾する。また、真だとすると命題自身が述べるように証明できないことになる。ゲーデルはこの命題を定式化することで、真であっても証明不可能な問題が存在することを示したわけである。
フェルマー予想に取り組んでいて不完全性定理を知った数学者の中には、「もしかしたらフェルマー予想はそもそも証明不可能なのかもしれない」と考え始めた者もいたという。
近代的アプローチ
根本的な解決がなされないまま、フェルマーの予想から300年という時が流れた。その間、無数の数学者が中学生でも理解できるこの命題の魔力に惹かれ挑戦したが、全員が敗れ去っていった。
1930年代ころまでには証明に使えそうな手法も底をついており、現代数学の本流から外れた時代遅れのフェルマー予想にまともに取り組もうとする数学者はいなくなっていた。
「無限」という果てなき相手を前に絶望的かに思えた数学者達の挑戦であったが、この物語は20世紀後半に意外な場所で突然最終章に突入する。
その舞台となった場所は
日本
1945年に第2次世界大戦が終了後、国土は荒れ果てていたが、戦争から解放された若い学生達は貪欲に学習した。この中には、フェルマー予想の証明のみならず現代数学の発展に多大な貢献をすることになる2人の東大生、谷山豊と志村五郎がいた。
1953年に東大を卒業して翌年に助手となった谷山豊は、1955年に日光で開かれた国際シンポジウムで「全ての楕円曲線はモジュラーである」という予想を発表し、世界から集まった数学者達の度肝を抜いた。楕円曲線とモジュラーは全く別分野の概念であるが、実質的に同じものではないかというとてつもない予想である。なお、楕円曲線とは y2=x3+ax2+bx+c で定まる曲線のことで、楕円とは無関係である。
この「谷山予想」は発表当初は全く信用されなかったが、1960年代に盟友の志村五郎(1930-2019)が積み上げた証拠のおかげで広く信じられていき、「谷山=志村予想」と呼ばれるようになった。知らない数学者はいないと言われるほど現代数学において計り知れない重要さを持つ予想であり、谷山=志村予想の証明が数学界の最大の目標の1つとなった。証明されていなかったにもかかわらず、谷山=志村予想が正しいという仮定のもと20年間で数百の論文が発表された。もしも谷山=志村予想が間違っていた場合、それらの論文は全てゴミとなる。数学者達は、誰かが証明し土台を確固たるものにしてくれることを渇望していた。
1927年、谷山豊は埼玉県で生を受けた。家族以外は大抵「ゆたか」と呼び間違えたため、自分でも「ゆたか」と名乗るようになった。世界的には「ユタカ・タニヤマ」の名で知られている。
子供時代は体が弱く、高校も2年間休学した。さらに第2次世界大戦の勃発もあり、東京大学理学部数学科に入ったのは1950年23歳のときであった。
天才肌であった谷山は、1953年に大学を卒業すると翌年には助手となる。1954年頃に2つ年下の志村五郎と出会い、共同研究も行うようになった。
前述した通り、1955年に「谷山予想」を発表した。1958年4月には助教授となり、10月には鈴木美佐子と婚約し、「何があっても決して離れない」と誓い合った。アメリカのプリンストン高等研究所からも招聘され、数学者人生の絶頂期を迎えていた。
しかし、突然恐ろしい破滅が訪れる。
1958年11月17日、池袋の静山荘20号室で谷山は自らその生涯に幕を下ろした(31歳)。ノート3ページにわたる遺書の冒頭には「最近精神的に参っている」「将来に対する自信を失った」「わがままを許してほしい」などと書き残されていた。志村は激しい後悔の念に苛まれたが、明確な理由は思い当たらなかったという。
悲劇は日本最高の頭脳が永久に失われてしまっただけに留まらなかった。
二週間後の12月2日、静山荘の近くのアパートで婚約者の鈴木美佐子が後を追った。「私たちは誓い合ったのだから」という旨の遺書を残して―。
翌年の1月25日に葬婚式が行われ、現在は埼玉県善応寺で二人一緒に眠っている。
フェルマー予想再び!
1984年、ゲルハルト・フライ(ドイツ)は、フェルマー予想がもし間違っていたら、つまりもし仮に解を持つとしたらどうなるのかと考え仮想的な解を代入していった。すると、モジュラーではない異常な楕円曲線が現れた。これは、すべての楕円曲線がモジュラーであるとする谷山=志村予想に反する。すなわち
「フェルマー予想が偽ならば、谷山=志村予想も偽である」
とすると、これの対偶は・・・
「谷山=志村予想が真ならば、フェルマー予想も真である」
この瞬間、フェルマー予想の証明は谷山=志村予想の証明に移り代わった。現代数学の片隅に追いやられて骨董品となっていたフェルマー予想が、谷山=志村予想に姿を変えて現代数学の本流に戻ってきたのである。
とはいえ、すでの谷山予想の発表から30年もの間数学者達は敗北を繰り返してきており、その攻略は絶望視され無謀な戦いに挑もうとする数学者は現れなかった。
ただ1人の天才を除いては・・・。
アンドリュー・ワイルズによる最終証明
アンドリュー・ワイルズ(1953-;イギリス)は1963年10歳の時にフェルマー予想を知り、自分が証明することを夢見て数学者になった。
Required text: “copyright C. J. Mozzochi, Princeton N.J”, Attribution, via Wikimedia Commons
1975年、ケンブリッジ大学の院生となったワイルズに指導教官ジョン・コーツが与えた研究テーマは「楕円曲線」であった。子供の頃の夢は封印して現代数学の主流である楕円曲線の研究に打ち込み、やがてアメリカのプリンストン大学で教授になった。
1986年、自分の専門分野である楕円曲線がフェルマー予想と結びついたと聞いたワイルズは、大きな衝撃を受け、すぐに決断した。フェルマー予想と無関係な研究をすべて止め、谷山=志村予想の証明に自分の人生を賭けることにしたのである。その後7年間自宅の屋根裏部屋にこもり、単独でフェルマー予想の証明に没頭することになる。
ワイルズは、過去の数学者達の失敗を教訓に、以下のドミノ倒しのような論法を用いて、無限に存在するすべての楕円曲線の1つ1つが無限に存在するモジュラーの1つ1つに対応することを証明する戦略を立てた。
- 最初の1つが成り立つことを示す。
- 1つが成り立てばその次もまた成り立つことを示す。
そう、高校生もご存じの数学的帰納法である。
ワイルズは、19世紀悲劇の天才エヴァリスト・ガロアによって構築された「ガロア理論」を用いて最初の1つが成り立つことを証明した。これは最初の一歩であったが、本格的にフェルマー予想の証明に取り組みだしてからすでに2年が経過していた。

エヴァリスト・ガロアは、1811年フランス・パリ郊外の村で公立学校の校長(後に町長)である父と当時としては珍しく教養深い女性であった母の間に生まれ、12歳で学校に通い始めるまで母に教育を受けていた。
15歳のとき、初めて数学の授業を受け、教科書として使われていたルジャンドルの『幾何学原論』に出会ってガロアは数学に目覚めた。通常は習熟に2年かかると言われている『幾何学原論』を2日で読破したとの伝説が残っている。それ以降の数学への熱中ぶりは凄まじく、すぐに教師の手に負えなくなり、当時の数学者による最新の著作から直接学ぶようになった。
数学に狂気じみた情熱を抱き、圧倒的な才能を秘めていたガロアだったが、激情型の性格で革命家として政治的な活動にも参加していたことが数学史上最悪の悲劇へとつなっていく。
1828年、16歳になったガロアは教師の忠告を無視してパリにある最高学府「エコール・ポリテクニーク(高等理工科学校)」の入試を1年早く、準備もせずに受けたが、当然不合格に終わった。
その一方で、すでに「5次方程式の解」という世界最先端の難問に取り組んでいた。
2次方程式の解の公式は紀元前3000年頃のメソポタミア文明の時代から知られていたが、3次方程式と4次方程式の解の公式が発見されたのは16世紀になってからであった。当然次は5次方程式の解の公式の番であるが、200年もの間発見することが出来なかった。
18世紀の終わり頃には、5次以上の方程式にはそもそも代数的な解の公式は存在しないらしいことがわかってきていた。1824年になってようやく22歳の若き数学者ニールス・アーベル(ノルウェー)がこれを完全に証明した。
1829年、17歳のガロアは「代数方程式が代数的に解けるための必要十分条件は何か」について決定的な結果を得ていたという。後に「ガロア理論」と呼ばれ、近代数学の歴史を塗り替えることになる壮大な理論で、当時の水準を遙かに凌駕していた。この理論さえあればもはやアーベル論文の内容は明らかなのであった。
しかし、この年からガロアの運命の歯車が狂い出す。
最初の論文をパリ・アカデミーに送るも、行方不明になってしまう。7月に思想的に対立する司祭の画策の結果精神的に追い込まれた父親が自殺、その2日後には二度目のエコール・ポリテクニークの入試があったが再び失敗した。同じ学校の入試を受けられるのは2回までであったため、格下のエコール・ノルマルに進学した。
その数ヶ月後、再び論文をアカデミーの対象に応募するも、この論文もまた失われてしまう。実際のところは不明だが、ガロアはこれらの不運が政治的理由による故意のものだと考えるようになった。
それ以来、共和主義的な政治観を元に無鉄砲で過激な行動を繰り返すようになる。学長に個人攻撃する手紙を送って学校は退学処分、国民軍砲兵隊に加わるなどして三度にわたって逮捕された。
1831年、三度目の逮捕前に三度目の論文をアカデミーに送っていたが、逮捕後に獄中で「説明不十分」として却下され、ガロアは怒り狂った。ガロアの理論の重要性・先見性は当時世界最高の研究機関であったパリ科学アカデミーでさえ理解することはできなかった。
そして、悲劇の年を迎える。ガロアの最後の数ヶ月については謎が多く、一説には次のような話がある。
1832年3月に釈放されたガロアは、1人の女性の虜になるも、この女性は既に婚約済みで、婚約者に決闘を申し込まれた。5月29日、友人への手紙に「つまらない色女に引っかかって決闘を申し込まれた」という旨を記している。 自分の死を覚悟したガロアは、徹夜でガロア理論や楕円関数論に関する数学的な発想を必死に書き残した。「僕には時間がない」という悲痛な走り書きとともにー。そして30日早朝、パリ近郊で行われた決闘で破れたガロアは、翌日に腹膜炎によって息を引き取った。
決闘の理由や相手については複数の説があるが、数学史に残る若き天才数学者の頭脳が決闘などというおよそ価値の釣り合わない出来事によって永遠に失われたという事実は疑いようがない。ガロアが本格的に数学を始めてからわずか5年後のことであった。
友人や弟は遺書に従って19世紀最大の数学者ガウスやヤコビらに論文を送った。彼らにすら理解されなかったが、死後14年経って、論文を入手したリューヴィルがガロア理論の重要性に気づき、論文を著名な雑誌に発表したことで多くの数学者の目に止まるようになった。
ガロア理論は、現代数学の扉を開くとともに、20世紀、21世紀科学のあらゆる分野に絶大な影響を与えている。群論の基礎概念とも言える集合論がゲオルク・カントールによって提唱され、ガロア理論へと通じる数学領域が構築されるのでさえ、ガロアによるガロア理論構築の50年も後のことである。死後65年経ってガロア全集が発表され、さらに死後100年以上経って物理学に応用された。日本では大学の数学科の学生が3年生になってから学習する。
2. の証明はさらに難しく、2年間過去の論文にあったあらゆるアイディアやテクニックを試すも、すべて徒労に終わった。
それでもさらに1年間の忍耐を重ね、ジョン・コーツのもとで学んだ楕円曲線の分析手段の「岩澤理論」に期待を持ち始めるも、1991年の夏にはその期待も失われた。
5年間事実上の隠遁生活を送ってきたワイルズは、最新の情報を入手しようと考え、楕円曲線の主要な研究者達が集まる会議に参加した。そこでかつての師であるジョン・コーツからコリヴァギン=フラッハ法なるものが最近開発されたことを聞いた。これはまさにワイルズが求めていたものであった。
コリヴァギン=フラッハ法はそのままでは不十分であったが、ワイルズはこれを拡張し、1993年5月末についに谷山=志村予想の証明を完成させた。
ちょうど1993年6月末に故郷のケンブリッジのニュートン研究所で専門家会議が行われると知り、ここで証明を世界に向けて発表することにした。
ワイルズには3回の講演枠が割り振られた。ワイルズは講演の最終目標を明かしていなかったにもかかわらず、回を重ねるにつれて「フェルマー予想が証明される」との噂が広まっていった。
1993年6月23日、3回目の講演のときにはワイルズの証明を支える理論を生み出した数学者達のほとんど全員がその場にそろっていた。歴史的な講演を見逃すまいとケンブリッジ大学数学科の全員も集まり講演会場は超満員、あぶれた人々は窓からのぞき込んだ。講演も終わりに近づくと、多くの人が写真を撮り始めた。ワイルズは最後に黒板にフェルマーの最終予想を書き、「ここで終わりにしたいと思います」と締めくくった。拍手喝采がわき起こり、いつまでも止まなかった。「フェルマー予想証明」の大ニュースは世界中を駆け巡り、一流紙の一面を飾った。ワイルズは一夜にして世界で最も有名な数学者となったのであった。
マスコミがお祭り騒ぎをする中、数学者達は査読を始めていた。当然ながら講演しただけでは実際に証明したことにはならず、専門誌に論文を提出し、他の数学者による徹底的な検証を受けて正しいことが認められなければならない。
ワイルズは何の問題もなく検証が完了することを期待していたが、フェルマー予想はそう簡単に幕引きさせてはくれなかった。
8月、ワイルズの論文のコリヴァギン=フラッハ法に関する部分に1ヶ所重大な欠陥が見つかった。ワイルズは数学界に気付かれる前に証明を修正しようと努力したが、当初講演から数週間後に出されるはずであった論文が数ヶ月経っても出されず、そうこうしているうちに数学界には「ワイルズ証明に欠陥発覚」との噂がはびこり始めた。
栄光と喝采からわずか2ヶ月、ワイルズは衆人環視の元で証明の修正を強いられるという地獄のような日々を送ることになった。徐々に不完全でも論文を公開すべきだという周囲の圧力が大きくなってきたが、ワイルズは頑なにそれを拒んだ。足りていないのは最後のワンピースだけなのだ。そんな状態で論文を発表しようものなら、最後のワンピースを見つけて「フェルマー予想の完全証明者」の栄誉をかっさらおうとする数学者がゾンビのように群がってくるのは目に見えている。コリヴァギン=フラッハ法に熟達した教え子のリチャード・テイラーの協力も得たが、1年経過しても修正することができず、ワイルズは敗北宣言を覚悟しつつあった。
そんなワイルズに運命の日が訪れる。1994年9月19日、ワイルズは諦めをつけるためになぜコリヴァギン=フラッハ法がうまくいかなかったのかを吟味していた。すると突然、まったく不意に信じられないような閃きがあり、最後のワンピースを見つけることができたのだという。ワイルズはテレビカメラの前で涙ぐみながらそう当時を振り返った。
その最後のワンピースとは
岩澤理論
コリヴァギン=フラッハ法と岩澤理論はいずれもそれだけでは不十分だが、互いを補い合うことで完全なものになったのであった。
ワイルズは1994年10月に合計130ページに及ぶ二篇の論文を発表、1995年2月に誤りがないことが確認された。フェルマーの最終予想から360年、もはや予想ではなくなり、フェルマーの最終定理となった。
アンドリュー・ワイルズ『モジュラー楕円曲線とフェルマーの最終定理』(pdf)
リチャード・テイラー、アンドリュー・ワイルズ『ある種のヘッケ環の理論的性質』(pdf)
谷山の死後37年経過していたが、志村五郎は谷山=志村予想が証明される時代に居合わせることができた。感想を求められた志村は、穏やかに微笑みながら答えた。
「I told you so.(だから言ったでしょう)」
ワイルズの証明はそれまでの数論の進歩の集大成とも言える内容で、その過程では谷山豊、志村五郎、岩澤健吉、肥田晴三、加藤和也ら日本人数学者も大きく貢献した。
参考文献
以上、350年間のフェルマー予想の歴史の概略を紹介したが、詳細についてはサイモン・シンを読んでみてほしい。

面白すぎて読み終わるまで眠れないw












