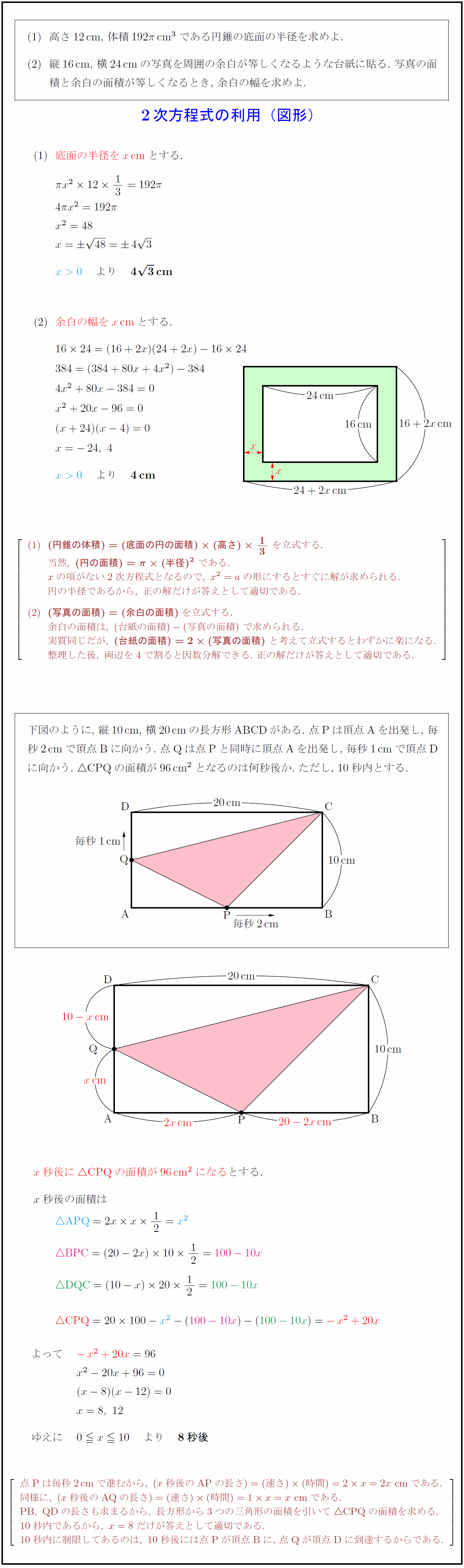
高さ12cm,\ 体積$192π$cm$³$である円錐の底面の半径を求めよ. 縦16cm,\ 横24cmの写真を周囲の余白が等しくなるような台紙に貼る.\ 写真の面積と余白の面積が等しくなるとき,\ 余白の幅を求めよ. 2次方程式の利用(図形)底面の半径を$x$cm}とする. (円錐の体積)=(底面の円の面積)(高さ)13}\ を立式する. 当然,\ {(円の面積)=π(半径)²}\ である. xの項がない2次方程式となるので,\ x²=aの形にするとすぐに解が求められる. 円の半径であるから,\ 正の解だけが答えとして適切である. {(写真の面積)=(余白の面積)}を立式する. 余白の面積は,\ (台紙の面積)-(写真の面積)\ で求められる. 実質同じだが,\ {(台紙の面積)=2(写真の面積)}\ と考えて立式するとわずかに楽になる. 整理した後,\ 両辺を4で割ると因数分解できる.\ 正の解だけが答えとして適切である. 下図のように,\ 縦10cm,\ 横20cmの長方形ABCDがある.\ 点Pは頂点Aを出発し,\ 毎 秒2cmで頂点Bに向かう.\ 点Qは点Pと同時に頂点Aを出発し,\ 毎秒1cmで頂点D に向かう.\ $$CPQの面積が96cm$²$となるのは何秒後か.\ ただし,\ 10秒内とする. 点 Pは毎秒2cm}で進むから,\ (x秒後のAP}の長さ)=(速さ)(時間)=2 x=2x\ cm}である. 同様に,\ (x秒後のAQ}の長さ)=(速さ)(時間)=1 x=x\ cm}である. {PB,\ QD}の長さも求まるから,\ 長方形から3つの三角形の面積を引いて{CPQ}の面積を求める. 10秒内であるから,\ x=8だけが答えとして適切である. 10秒内に制限してあるのは,\ 10秒後には点Pが頂点Bに,\ 点Qが頂点D}に到達するからである.

