デンプン（多糖類）
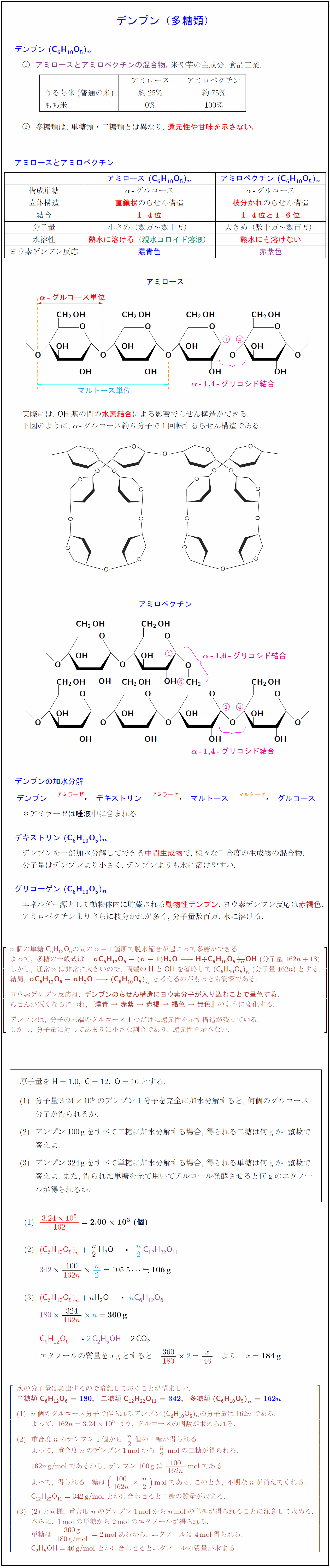
デンプン (C₆H₁₀O₅)ₙ
① アミロースとアミロペクチンの混合物. 米や芋の主成分. 食品工業.
| | アミロース | アミロペクチン |
|————|————|—————-|
| うるち米 | 約25% | 約75% |
| もち米 | 0% | 100% |
② 多糖類は、単糖類・二糖類とは異なり、還元性や甘味を示さない.
アミロースとアミロペクチン
| | アミロース (C₆H₁₀O₅)ₙ | アミロペクチン (C₆H₁₀O₅)ₙ |
|————|————————-|——————————|
| 構成単糖 | α-グルコース | α-グルコース |
| 立体構造 | 直鎖状のらせん構造 | 枝分かれのらせん構造 |
| 結合 | 1–4位 | 1–4位と1–6位 |
| 分子量 | 小さめ（数万～数十万） | 大きめ（数十万～数百万） |
| 水溶性 | 熱水に溶ける（親水コロイド溶液） | 熱水にも溶けない |
| ヨウ素反応 | 濃青色 | 赤紫色 |
アミロースの構造
実際には直鎖状ではなく、OH基の間の水素結合による影響でらせん構造ができる.
下図のように、α-グルコース単位6個で1回転するらせん構造である.
デンプンの加水分解
デンプン →[アミラーゼ（だ液）]→ デキストリン →[アミラーゼ（だ液）]→ マルトース →[マルターゼ（小腸）]→ グルコース
（多糖） →（多糖）→（二糖）→（単糖）
デンプン →[希酸]→ グルコース
デキストリン (C₆H₁₀O₅)ₙ
デンプンを一部加水分解してできる中間生成物で、様々な重合度の生成物の混合物.
分子量はデンプンより小さく、デンプンよりも水に溶けやすい. 酒造原料や糊.
グリコーゲン（動物デンプン） (C₆H₁₀O₅)ₙ
余剰グルコースをエネルギー源として貯蔵するために作られ、肝臓や筋肉に多く含まれる.
球状分子で、ヨウ素デンプン反応は赤褐色.
アミロペクチンよりさらに枝分かれが多く、分子量数十万～一千万だが、水に溶ける.
n個の単糖C₆H₁₂O₆ の間の n−1 箇所で脱水縮合が起こって多糖ができる.
よって、多糖の一般式は
n C₆H₁₂O₆ − (n−1) H₂O → H−(C₆H₁₀O₅)ₙ−−OH (分子量 162n + 18)
しかし、通常 n は非常に大きいので、両端の H と OH を省略して
(C₆H₁₀O₅)ₙ (分子量 162n) とする.
結局、n C₆H₁₂O₆ − n H₂O → (C₆H₁₀O₅)ₙ と考えればよい.
デンプンには、分子の末端のグルコース1つだけに還元性を示すヘミアセタール構造が残っている.
しかし、分子量に対してあまりに小さな割合なので、還元性を示さない.
デンプンを熱水につけておくと、水溶性のアミロースは溶けて不溶性のアミロペクチンは沈殿する.
アミロースは多数の親水性のOH基をもつが、分子内水素結合に使われるため、冷水には溶けない.
熱水では分子内水素結合が切れて溶け出し、親水コロイド溶液となる.
アミロペクチンは分子量が大きく、枝分かれ構造で水分子が内に入り込みにくいため熱水でも溶けない.
ヨウ素デンプン反応は、デンプンのらせん構造にヨウ素分子が入り込むことで呈色する.
らせんが短くなるにつれ、「濃青 → 赤紫 → 赤褐 → 褐色 → 無色」のように変化する.
ブドウ糖(グルコース)は植物の光合成で作られるが、水に溶けやすく、そのままでは雨で流出する.
そこで、植物は水に溶けにくいデンプン(多糖)の形にしてグルコースを種子や根に蓄えている.
デンプンを食物として摂取すると、消化酵素で加水分解され、グルコースとして体内に吸収される.
グルコースは各器官で消費され、その燃焼熱が生物のエネルギー源となる.
C₆H₁₂O₆ + 6O₂ → 6CO₂ + 6H₂O ΔH = −2803 kJ
なお、希酸を用いると、一気にグルコースまで加水分解される.
グリコーゲンは必要に応じ加水分解されてグルコースとなり、血液中のグルコース濃度を一定に保つ.
グリコーゲンの形で貯蔵するのは、重合すると物質量(個数)が小さくなり、
浸透圧を上げずにグルコースを多数貯蔵できるからである
(浸透圧が上がりすぎると細胞に悪影響).
浸透圧 Π は溶質粒子のモル濃度 C[mol/L] に比例するのであった (ファントホッフの法則 Π = CRT).
仮に重合度1万のグリコーゲン1個をグルコース1万個にすると、浸透圧(モル濃度)も1万倍になる.
早い話、バラバラで貯蔵するよりもまとめて貯蔵する方が合理的というわけである.
原子量を H = 1.0, C = 12, O = 16 とする.
(1) 分子量 3.24×10⁵ のデンプン1分子を完全に加水分解すると、何個のグルコース分子が得られるか.
(2) デンプン100 g をすべて二糖に加水分解する場合、得られる二糖は何 g か. 整数で答えよ.
(3) デンプン324 g をすべて単糖に加水分解する場合、得られる単糖は何 g か.
また、得られた単糖を全て用いてアルコール発酵させると何 g のエタノールが得られるか.
(1) 3.24×10⁵ ÷ 162 = 2.00×10³ (個)
(2) (C₆H₁₀O₅)ₙ + (n/2) H₂O → (n/2) C₁₂H₂₂O₁₁
得られる二糖は
342 × (100 / (162n)) × (n/2) = 105.5… ≈ 106 g
(3) (C₆H₁₀O₅)ₙ + n H₂O → n C₆H₁₂O₆
得られる単糖は
180 × (324 / (162n)) × n = 360 g
C₆H₁₂O₆ → 2 C₂H₅OH + 2 CO₂
エタノールの質量を x[g] とすると
(360 / 180) × 2 = x / 46
より x = 184 g
[解説補足]
次の分子量は頻出するので暗記しておくことが望ましい.
単糖類 C₆H₁₂O₆ = 180
二糖類 C₁₂H₂₂O₁₁ = 342
多糖類 (C₆H₁₀O₅)ₙ = 162n
(二糖類) = (単糖類)×2 − H₂O = 180×2 − 18 = 342 という関係も重要である.
(1) n個のグルコース分子で作られるデンプン (C₆H₁₀O₅)ₙ の分子量は162nである.
よって 162n = 3.24×10⁵ より、グルコースの個数が求められる.
(2) 重合度 n のデンプン1個から (n/2) 個の二糖が得られる.
よって、重合度 n のデンプン1 mol から (n/2) mol の二糖が得られる。
デンプンは 162n g/mol であるから、デンプン100 g は 100/(162n) mol である。
よって、得られる二糖は (100/(162n) × n/2) mol である。
このとき、不明な n が消えてくれる。
一定質量の多糖から得られる二糖の物質量や質量は、重合度 n によらず一定である。
C₁₂H₂₂O₁₁ = 342 g/mol と掛け合わせると二糖の質量[g]が求まる.
(3) (2) と同様、重合度 n のデンプン1 mol から n mol の単糖が得られる.
さらに、1 mol の単糖から 2 mol のエタノールが得られる.
単糖は 360 g / 180 g/mol = 2 mol あるから、エタノールは 4 mol 得られる.
C₂H₅OH = 46 g/mol と掛け合わせるとエタノールの質量[g]が求まる.
